题目内容
19.已知函数f(x)=log2$\frac{2x^2}{x^2+1}$(x>0),若函数g(x)=f(x)2+m$|\begin{array}{l}{f(x)}\end{array}|$+2m+3有三个不同的零点,则实数m的最大值为( )| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
分析 先判断函数f(x)的单调性和取值范围,利用换元法,设|f(x)|=t,则函数g(x)=f(x)2+m$|\begin{array}{l}{f(x)}\end{array}|$+2m+3有三个不同的零点转化为对应方程有三个不同的实数解,即为t2+mt+2m+3=0有两个根,且一个在(0,1)上,一个在[1,+∞)上,由此可得结论.利用根的分布进行求解即可.
解答 解:∵$\frac{2x^2}{x^2+1}$=$\frac{2({x}^{2}+1)-2}{{x}^{2}+1}$=2-$\frac{2}{{x}^{2}+1}$,
∴当x>0时y=$\frac{2x^2}{x^2+1}$为增函数,且y=$\frac{2x^2}{x^2+1}$∈(0,2),
则f(x)为增函数,且f(x)∈(-∞,1),
设t=f(x),则t<1,
则函数g(x)=f(x)2+m$|\begin{array}{l}{f(x)}\end{array}|$+2m+3有三个不同的零点,等价为y=t2+m|t|+2m+3在t<1时有三个不同的零点,
y=|f(x)|大致图象如图所示,
即方程|t|2+m|t|+2m+3=0有三个不同的实数解,即为t2+mt+2m+3=0有两个根,且一个在(0,1)上,一个在[1,+∞)上,
设h(t)=t2+mt+2m+3,
①当有一个根为1时,h(1)=12+m+2m+3=0,$m=-\frac{4}{3}$,此时另一根为$\frac{1}{3}$适合题意;
②当没有根为1时,$\left\{\begin{array}{l}h(0)>0\\ h(1)<0\end{array}\right.$,得$\left\{\begin{array}{l}2m+3>0\\{1^2}+m+2m+3<0\end{array}\right.$,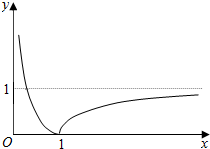
∴$-\frac{3}{2}<m<-\frac{4}{3}$,
综上-$\frac{3}{2}$<m≤-$\frac{4}{3}$;
∴实数m的最大值为的取值范围为-$\frac{4}{3}$;
故选:B.
点评 本题考查了复合函数的应用及方程的根与函数的零点的关系应用,考查运算能力,利用数形结合以及换元法和转化法是解决本题的关键.综合性较强,有一定的难度.

| A. | $\frac{π}{6}$ | B. | 1-$\frac{π}{6}$ | C. | $\frac{π}{12}$ | D. | 1-$\frac{π}{12}$ |
| A. | f(x)在区间[0,$\frac{π}{2}$]内是增函数 | |
| B. | 若?x1≠x2,f(x1)=f(x2)=0,则x1-x2必是π的整数倍 | |
| C. | f(x)的图象关于点(-$\frac{π}{12}$+$\frac{kπ}{2}$,0)(k∈Z)对称 | |
| D. | f(x)的图象关于直线x=$\frac{π}{12}$对称 |
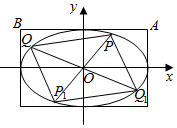 (重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$
(重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$