题目内容
11. (重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$
(重点中学做)已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点(3,1),离心率e=$\frac{\sqrt{6}}{3}$(1)求椭圆C的方程;
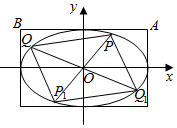
(2)分别过椭圆C的四个顶点作坐标轴的垂线,围成如图所示的矩形,A,B是所围成的矩形在x轴上方的两个顶点.若P,Q是椭圆C上两个动点,直线OP、OQ与椭圆的另一交点分别为P1、Q1,且直线OP、OQ的斜率之积等于直线OA、0B的斜率之积,试问四边形PQP1Q1的面积是否为定值?若为定值,求出其值;若不为定值,说明理由(0为坐标原点).
分析 (1)由离心率公式和点满足椭圆方程,解方程可得a,b,进而得到椭圆方程;
(2)由题意可得,四条垂线的方程为x=±2$\sqrt{3}$,y=±2,A(2$\sqrt{3}$,2),B(-2$\sqrt{3}$,2),可得kOA•kOB=-$\frac{1}{3}$,设P(x1,y1),Q(x2,y2),运用椭圆方程,求得x12+x22=12,讨论若x1=x2,若x1≠x2,运用点到直线的距离公式和三角形的面积公式,以及椭圆的对称性,计算即可得到所求面积为定值.
解答 解:(1)由e=$\frac{\sqrt{6}}{3}$,可得$\frac{{b}^{2}}{{a}^{2}}$=$\frac{{a}^{2}-{c}^{2}}{{a}^{2}}$=1-e2=$\frac{1}{3}$,即a2=3b2,
又$\frac{9}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1,解得a=2$\sqrt{3}$,b=2,
即有椭圆的方程为$\frac{{x}^{2}}{12}$+$\frac{{y}^{2}}{4}$=1;
(2)由题意可得,四条垂线的方程为x=±2$\sqrt{3}$,y=±2,
A(2$\sqrt{3}$,2),B(-2$\sqrt{3}$,2),
可得kOA•kOB=-$\frac{1}{3}$,
设P(x1,y1),Q(x2,y2),则$\frac{{y}_{1}{y}_{2}}{{x}_{1}{x}_{2}}$=-$\frac{1}{3}$,|PQ|=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$,
由P,Q在椭圆上,可得y12=4(1-$\frac{{{x}_{1}}^{2}}{12}$),y22=4(1-$\frac{{{x}_{2}}^{2}}{12}$),
由x12x22=9y12y22=(12-x12)(12-x22),即有x12+x22=12,
若x1=x2,则P,P1,Q,Q1分别是直线OA,OB与椭圆的交点,
四个点的坐标为($\sqrt{6}$,$\sqrt{2}$),(-$\sqrt{6}$,-$\sqrt{2}$),(-$\sqrt{6}$,$\sqrt{2}$),($\sqrt{6}$,-$\sqrt{2}$),
四边形PQP1Q1的面积为8$\sqrt{3}$;
若x1≠x2,则直线PQ:y-y1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),
化为(y2-y1)x-(x2-x1)y+x2y1-x1y2=0,
则O到直线PQ的距离为d=$\frac{|{x}_{1}{y}_{2}-{x}_{2}{y}_{1}|}{\sqrt{(({y}_{2}-{y}_{1})^{2}+({x}_{2}-{x}_{1})^{2}}}$,
即有△OPQ的面积为S=$\frac{1}{2}$|PQ|•d=$\frac{1}{2}$|x1y2-x2y1|=$\frac{1}{2}$$\sqrt{{{x}_{1}}^{2}{{y}_{2}}^{2}-2{x}_{1}{x}_{2}{y}_{1}{y}_{2}+{{x}_{2}}^{2}{{y}_{1}}^{2}}$
=$\frac{1}{2}$$\sqrt{4{{x}_{1}}^{2}(1-\frac{{{x}_{2}}^{2}}{12})+\frac{2}{3}({x}_{1}{x}_{2})^{2}+4{{x}_{2}}^{2}(1-\frac{{{x}_{1}}^{2}}{12})}$=$\frac{1}{2}$$\sqrt{4({{x}_{1}}^{2}+{{x}_{2}}^{2})}$=2$\sqrt{3}$,
由椭圆的对称性可得,四边形PQP1Q1的面积为4S=8$\sqrt{3}$.
综上可得,四边形PQP1Q1的面积定值8$\sqrt{3}$.
点评 本题考查椭圆的方程的求法,注意运用离心率公式和点满足椭圆方程,考查四边形面积是否为定值,注意运用分类讨论的思想方法,运用点到直线的距离公式和三角形的面积公式,考查化简整理的运算能力,属于难题.

 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
| A. | [$\frac{3}{2}$,+∞) | B. | [2$\sqrt{2}$-3,+∞) | C. | [2$\sqrt{2}$-3,$\frac{56}{9}$] | D. | [$\frac{3}{2}$,$\frac{56}{9}$] |