题目内容
10.在Rt△ABC中,∠A为直角,且AB=3,BC=5,若在三角形ABC内任取一点,则该点到三个定点A,B,C的距离不小于1的概率是( )| A. | $\frac{π}{6}$ | B. | 1-$\frac{π}{6}$ | C. | $\frac{π}{12}$ | D. | 1-$\frac{π}{12}$ |
分析 根据条件作出对应的图象,求出对应的面积,根据几何概型的概率公式进行计算即可.
解答 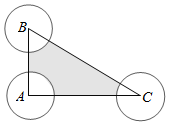 解:在Rt△ABC中,∠A为直角,且AB=3,BC=5,
解:在Rt△ABC中,∠A为直角,且AB=3,BC=5,
∴AC=4,则△ABC的面积S=$\frac{1}{2}×3×4$=6,
若在三角形ABC内任取一点,则该点到三个定点A,B,C的距离不小于1,
则该点位于阴影部分,
则三个小扇形的圆心角转化为180°,半径为1,则对应的面积之和为S=$\frac{π×{1}^{2}}{2}$=$\frac{π}{2}$,
则阴影部分的面积S=6-$\frac{π}{2}$,
则对应的概率P=$\frac{{S}_{阴影}}{{S}_{△ABC}}$=$\frac{6-\frac{π}{2}}{6}$=1-$\frac{π}{12}$,
故选:D.
点评 本题主要考查几何概型的概率的计算,根据条件求出对应区域的面积是解决本题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
20.在如下程序框图中,已知f0(x)=sinx,则输出的结果是( )


| A. | sinx | B. | cosx | C. | -sinx | D. | -cosx |
19.已知函数f(x)=log2$\frac{2x^2}{x^2+1}$(x>0),若函数g(x)=f(x)2+m$|\begin{array}{l}{f(x)}\end{array}|$+2m+3有三个不同的零点,则实数m的最大值为( )
| A. | $\frac{4}{3}$ | B. | -$\frac{4}{3}$ | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |