题目内容
4.函数y=$\frac{{x}^{2}-x+6}{{x}^{2}-2x-3}$的值域是(-∞,$-\frac{1}{4}-\frac{\sqrt{6}}{2}$]∪[$-\frac{1}{4}+\frac{\sqrt{6}}{2},+∞$).分析 把原函数解析式变形,化为关于x的方程,讨论二次项系数后利用判别式法求函数的值域.
解答 解:由y=$\frac{{x}^{2}-x+6}{{x}^{2}-2x-3}$,得(y-1)x2-(2y-1)x-(3y+6)=0.
当y=1时,x=-9;
当y≠1,由△=(2y-1)2+4(y-1)(3y+6)=16y2+8y-23≥0,
解得:$y≤-\frac{1}{4}-\frac{\sqrt{6}}{2}$或$y≥-\frac{1}{4}+\frac{\sqrt{6}}{2}$且y≠1.
∴函数y=$\frac{{x}^{2}-x+6}{{x}^{2}-2x-3}$的值域是(-∞,$-\frac{1}{4}-\frac{\sqrt{6}}{2}$]∪[$-\frac{1}{4}+\frac{\sqrt{6}}{2},+∞$).
故答案为:(-∞,$-\frac{1}{4}-\frac{\sqrt{6}}{2}$]∪[$-\frac{1}{4}+\frac{\sqrt{6}}{2},+∞$).
点评 本题考查函数的值域及其求法,训练了判别式法求函数的值域,是中档题.

练习册系列答案
相关题目
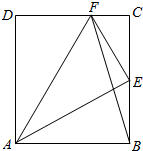 如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.
如图,在矩形ABCD中,点E是BC边上中点,点F在边CD上.