Question

14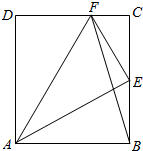．如图，在矩形ABCD中，点E是BC边上中点，点F在边CD上．
（1）若点F是CD上靠近C的三等分点，设$\overrightarrow{EF}$=λ$\overrightarrow{AB}$+$μ\overrightarrow{AD}$，求λ+μ的值．
（2）若AB=$\sqrt{3}$，BC=2，当$\overrightarrow{AE}$•$\overrightarrow{BF}$=1时，求DF的长．

Answer 1

分析 （1）根据向量的加减的几何意义即可求出；
（2）建立平面直角坐标系，设F（x，2），根据向量坐标的数量积求出x=$\frac{2\sqrt{3}}{3}$，即求出DF的长．

解答 解：（1）$\overrightarrow{EF}$=$\overrightarrow{AF}$-$\overrightarrow{AE}$=$\overrightarrow{AD}$+$\overrightarrow{DF}$-（$\overrightarrow{AB}$+$\overrightarrow{BE}$）=$\overrightarrow{AD}$+$\frac{2}{3}$$\overrightarrow{DC}$-（$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{BC}$）=$\overrightarrow{AD}$+$\frac{2}{3}$$\overrightarrow{AB}$-（$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$）=$\frac{1}{2}$$\overrightarrow{AD}$-$\frac{1}{3}$$\overrightarrow{AB}$=λ$\overrightarrow{AB}$+$μ\overrightarrow{AD}$，
∴λ=-$\frac{1}{3}$，μ=$\frac{1}{2}$，
∴λ+μ=$\frac{1}{6}$．
（2）以AB，AD为x，y轴建立直角坐标系如图：AB=$\sqrt{3}$，BC=2
则A（0，0），B（$\sqrt{3}$，0），E（$\sqrt{3}$，1），
设F（x，2），
∴$\overrightarrow{AE}$=（$\sqrt{3}$，1），$\overrightarrow{BF}$=（x-$\sqrt{3}$，2），
∵$\overrightarrow{AE}$•$\overrightarrow{BF}$=1，
∴$\sqrt{3}$（x-$\sqrt{3}$）+2=1，
∴x=$\frac{2\sqrt{3}}{3}$，
∴|DF|=$\frac{2\sqrt{3}}{3}$．

点评 本题考查向量的加减的几何意义和向量在几何中的应用，建立平面直角坐标系是解题的关键之一，考查计算能力．