题目内容
17.已知在递增等差数列{an}中,a3=1,a4是a3和a7的等比中项.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an}的前n项和为Sn,求该数列的前10项的和S10的值.
分析 (Ⅰ)由题意设出等差数列的公差,再由已知列式求得首项和公差,则数列{an}的通项公式可求;
(Ⅱ)直接由等差数列的前n项和公式得答案.
解答 解:(Ⅰ)在递增等差数列{an}中,设公差d>0,
由题意,$\left\{\begin{array}{l}{{a}_{1}+2d=1}\\{({a}_{1}+3d)^{2}={a}_{1}+6d}\end{array}\right.$,解得$\left\{\begin{array}{l}{{a}_{1}=-3}\\{d=2}\end{array}\right.$,
数列{an}的通项公式为an=2n-5;
(Ⅱ)由(Ⅰ)知,${S}_{10}=10×(-3)+\frac{10×9}{2}×2=60$.
点评 本题考查等差数列的通项公式,考查了等比数列的性质,训练了等差数列前n项和的求法,是中档题.

练习册系列答案
相关题目
5.下列函数中,是奇函数且在(0,+∞)上单调递增的为( )
| A. | y=x2 | B. | $y={x^{\frac{1}{3}}}$ | C. | y=x-1 | D. | $y={x^{-\frac{1}{2}}}$ |
12.在自变量的同一变化过程中,下列命题中正确的是( )
| A. | 若$\underset{lim}{x→{x}_{0}}$f(x)和$\underset{lim}{x→{x}_{0}}$g(x)都不存在,则$\underset{lim}{x→{x}_{0}}$[f(x)+g(x)]不存在 | |
| B. | 若$\underset{lim}{x→{x}_{0}}$f(x)和$\underset{lim}{x→{x}_{0}}$g(x)都不存在,则$\underset{lim}{x→{x}_{0}}$[f(x)g(x)]不存在 | |
| C. | $\underset{lim}{x→{x}_{0}}$$\frac{f(x)}{g(x)}$存在,且$\underset{lim}{x→{x}_{0}}$[g(x)]=0,则$\underset{lim}{x→{x}_{0}}$f(x)=0 | |
| D. | 若$\underset{lim}{x→{x}_{0}}$|f(x)|=|A|,$\underset{lim}{x→{x}_{0}}$f(x)=A. |
6.已知直线$x=\frac{π}{4}\;和\;x=\frac{5π}{4}$是函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)图象的两条相邻的对称轴,则φ的值为( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |
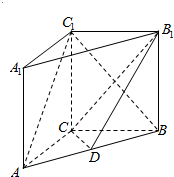 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=4,AA1=4,点D是AB的中点,
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=3,BC=4,AA1=4,点D是AB的中点, 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.求:
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E为AB的中点.求: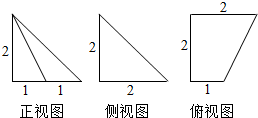 一个五面体的三视图如图,正视图是等腰直角三角形,侧视图是直角三角形,部分边长如图所示,则此五面体的体积为( )
一个五面体的三视图如图,正视图是等腰直角三角形,侧视图是直角三角形,部分边长如图所示,则此五面体的体积为( )