题目内容
如图,在长方形ABCD中,AB=2,BC=1,E为CD的中点,F为AE的中点.现在沿AE将三角形ADE向上折起,在折起的图形中解答下列两问:

(Ⅰ)在线段AB上是否存在一点K,使BC∥面DFK?若存在,请证明你的结论;若不存在,请说明理由;
(Ⅱ)若面ADE⊥面ABCE,求二面角E-AD-B的余弦值.

(Ⅰ)在线段AB上是否存在一点K,使BC∥面DFK?若存在,请证明你的结论;若不存在,请说明理由;
(Ⅱ)若面ADE⊥面ABCE,求二面角E-AD-B的余弦值.
考点:二面角的平面角及求法,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(Ⅰ)线段AB上存在一点K,且当AK=
AB时,BC∥面DFK.取H为AB的中点,连接EH,可得BC∥EH.利用三角形的中位线定理可证明FK∥EH,于是得到FK∥BC,再利用线面平行的判定定理即可证明;
(II)通过建立如图所示的空间直角坐标系,求出两个平面的法向量的夹角即可得出二面角.
| 1 |
| 4 |
(II)通过建立如图所示的空间直角坐标系,求出两个平面的法向量的夹角即可得出二面角.
解答:
解:(Ⅰ)线段AB上存在一点K,且当AK=
AB时,BC∥面DFK.
证明如下: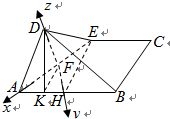
设H为AB的中点,连接EH,则BC∥EH
又∵AK=
AB,F为AE的中点
∴KF∥EH,∴KF∥BC,
∵KF?面DFK,BC?面DFK,∴BC∥面DFK.
(Ⅱ)∵H为AB的中点,∴AH=HE=BC=1,
∵F为AE的中点,∴FH⊥AE.
∵DA=DE=1,∴DF⊥AE,
∵面ADE⊥面ABCE,∴DF⊥面ABCE
由此可以FA,FH,FD分别为x,y,z轴,建立坐标系如图.
∵DF⊥面ABCE,∴DF⊥FH,
又∵FH⊥AE,DF∩AE=F,∴FH⊥面ADE,则
为面ADE的一个法向量.
∵AB=2,BC=1,∴FH=
,
=(0,
,0).
又可得:D(0,0,
),A(
,0,0),
∴
=(-
,0,
),
=(-
,
,0).
设面ADB的法向量为
=(x,y,z)
由
⇒
,即
,令x=1,则
=(1,1,1).
所以cos<
,
>=
=
,
故二面角E-AD-B的余弦值为
.
| 1 |
| 4 |
证明如下:

设H为AB的中点,连接EH,则BC∥EH
又∵AK=
| 1 |
| 4 |
∴KF∥EH,∴KF∥BC,
∵KF?面DFK,BC?面DFK,∴BC∥面DFK.
(Ⅱ)∵H为AB的中点,∴AH=HE=BC=1,
∵F为AE的中点,∴FH⊥AE.
∵DA=DE=1,∴DF⊥AE,
∵面ADE⊥面ABCE,∴DF⊥面ABCE
由此可以FA,FH,FD分别为x,y,z轴,建立坐标系如图.
∵DF⊥面ABCE,∴DF⊥FH,
又∵FH⊥AE,DF∩AE=F,∴FH⊥面ADE,则
| FH |
∵AB=2,BC=1,∴FH=
| ||
| 2 |
| FH |
| ||
| 2 |
又可得:D(0,0,
| ||
| 2 |
| ||
| 2 |
∴
| AD |
| ||
| 2 |
| ||
| 2 |
| AH |
| ||
| 2 |
| ||
| 2 |
设面ADB的法向量为
| n |
由
|
|
|
| n |
所以cos<
| FH |
| n |
| ||||||
|
| ||
| 3 |
故二面角E-AD-B的余弦值为
| ||
| 3 |
点评:熟练掌握三角形的中位线定理、线面平行的判定定理、通过建立如图所示的空间直角坐标系利用两个平面的法向量的夹角得出二面角是解题的关键.

练习册系列答案
相关题目
对于一切实数x不等式ax2+ax-2≤0恒成立,则a的取值范围为( )
| A、(8,0) |
| B、[-8,0] |
| C、(8,0] |
| D、[-8,0) |