Question

已知实数x，y满足：

x≥1 y≤2 x-y≤0

则（x-3）²+y²的最小值是

 

．

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

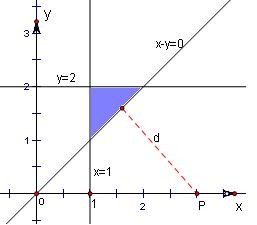
分析：作出不等式组表示的平面区域；通过（x-3）²+y²的几何意义：可行域内的点到（3，0）距离的平方；结合图象求出（3，0）到直线的距离即可．

解答： 解：∵变量x，y满足约束条件

x≥1 y≤2 x-y≤0

，
目标函数为：（x-3）²+y²，其几何意义是可行域内的点到（3，0）距离的平方；
点P（3，0）到直线x-y=0的距离公式可得：d=

|3-0|

2

，
结合图形可得（x-3）²+y²的最小值为：（

3

2

）²=

9

2

故答案为：

9

2

．

点评：本题考查画不等式组表示的平面区域、考查数形结合求函数的最值，此题是一道中档题，有一定的难度，画图是关键．