题目内容
12.有F列四个命题:①命题“若|x|≥2,则x≥2或x≤-2”的否命题;
②命题“面积相等的三角形全等”的否命题;
③命题“若m≤1,则x2-2x+m=0有实根”的逆否命题;
④命题“若A∩B=B,则A?B”的逆否命题.
其中是真命题的是①②③(填上你认为正确的命题的序号).
分析 ①命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”;
②“面积相等的三角形全等”的否命题为:面积不相等的三角形一定不全等,利用全等三角形的面积一定相等即可判断出;
③若x2-2x+m=0有实根则△=4-4m≥0,解得即可;
④“若A∩B=B,则A⊆B”不正确,利用其逆否命题与原命题等价即可得出.
解答 解:①命题“若|x|≥2,则x≥2或x≤-2”的否命题是“若|x|<2,则-2<x<2”,正确;
②命题“面积相等的三角形全等”的否命题是“面积不相等的三角形不全等”,正确;
③若x2-2x+m=0有实根则△=4-4m≥0,解得m≤1,因此正确;
④若A∩B=B,则B⊆A,因此“若A∩B=B,则A⊆B”不正确,其逆否命题也不正确.
综上可得:真命题的是①②③.
故答案为:①②③.
点评 本题考查了绝对值不等式、全等三角形面积之间的关系、一元二次方程由实数根与判别式的关系、集合之间的关系等基础知识与基本技能方法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.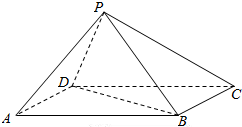 如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.
(I)证明:BD⊥PA;
(Ⅱ)求直线AP与平面PBC所成角的正弦值.
 如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.(I)证明:BD⊥PA;
(Ⅱ)求直线AP与平面PBC所成角的正弦值.
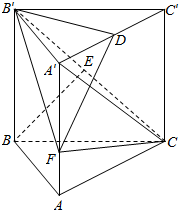 如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.
如图,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2,BB1=3,D为A1C1的中点,E为B1C的中点.