题目内容
8.在等比数列{an}中,a2•a6=3a4,a1=1.数列{bn}是等差数列,b1=a1,b7=a4,则b4=( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 由已知结合等比数列的性质求得a4,再由等差数列的性质求得b4 .
解答 解:在等比数列{an}中,由a2•a6=3a4,得${{a}_{4}}^{2}=3{a}_{4}$,
∵a4≠0,∴a4=3,
又数列{bn}是等差数列,且b1=a1,b7=a4,
∴b1=a1=1,b7=a4=3,
则${b}_{4}=\frac{{b}_{1}+{b}_{7}}{2}=\frac{1+3}{2}=2$.
故选:A.
点评 本题考查等比数列和等差数列的性质,是基础题.

练习册系列答案
相关题目
18.已知a=ln0.2,b=20.3,c=0.30.2,则实数a,b,c的大小关系为( )
| A. | a>b>c | B. | c>b>a | C. | b>c>a | D. | b>a>c |
17.某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:万元)对年销售量y(单位:吨)的影响,为此对近6年的年宣传费x(单位:万元)和年销售量y(单位:吨)的数据进行整理,得如下统计表:
(Ⅰ)由表中数据求得线性回归方程$\hat y=\hat bx+\hat a$中的$\hat b≈0.6$,试求出$\hat a$的值;
(Ⅱ)已知这种产品的年利润z(单位:万元)与x、y之间的关系为z=30y-x2,根据(Ⅰ)中所求的回归方程,求年宣传费x为何值时,年利润z的预估值最大?
| x(万元) | 2 | 3 | 4.5 | 5 | 7.5 | 8 |
| y(吨) | 3 | 3.5 | 3.5 | 4 | 6 | 7 |
(Ⅱ)已知这种产品的年利润z(单位:万元)与x、y之间的关系为z=30y-x2,根据(Ⅰ)中所求的回归方程,求年宣传费x为何值时,年利润z的预估值最大?
18.已知函数f(x)=2cos(ωx+φ)+1(ω>0,|φ|<$\frac{π}{2}$),其图象与直线y=3相邻两个交点的距离为$\frac{2π}{3}$,若f(x)>1对?x∈(-$\frac{π}{12}$,$\frac{π}{6}$)恒成立,则φ的取值范围是( )
| A. | [-$\frac{π}{6}$,$\frac{π}{6}$] | B. | [-$\frac{π}{4}$,0] | C. | (-$\frac{π}{3}$,-$\frac{π}{12}$] | D. | [0,$\frac{π}{4}$] |

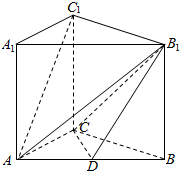 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.