题目内容
9.已知双曲线E:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1的一条渐近线过点(1,-1),则E的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 根据题意,由双曲线E的方程可得其渐近线方程为y=±$\frac{b}{a}$x,又由其一条渐近线过点(1,-1)可得$\frac{b}{a}$=1,进而由离心率计算公式e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$计算可得答案.
解答 解:根据题意,双曲线E的方程为:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1,其焦点在x轴上,
则其渐近线方程为y=±$\frac{b}{a}$x,
又由其一条渐近线过点(1,-1),则有$\frac{b}{a}$=1,
则E的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\sqrt{2}$;
故选:A.
点评 本题考查双曲线的几何性质,关键是依据题意,求出该双曲线渐近线的方程.

练习册系列答案
相关题目
19.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | α∥β,m⊥α,n∥β⇒m⊥n | D. | 若α⊥β,α∩β=n,m⊥n,则m⊥α |
20.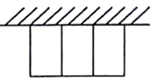 有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
 有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )| A. | 200m2 | B. | 360m2 | C. | 400m2 | D. | 480m2 |
4.在等比数列{an}中,已知a7•a19=8,则a3•a23=( )
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |