题目内容
11.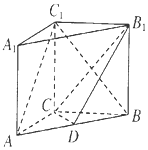 如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,三角形ABC为等腰直角三角形,AC=BC=$\sqrt{2}$,AA1=1,点D是AB的中点.(1)求证:AC1∥平面CDB1;
(2)二面角B1-CD-B的平面角的大小.
分析 (1)设BC1∩B1C=E,连接ED,则ED∥AC,由此能证明AC1∥平面CDB1.
(2)推导出CD⊥AB,BB1⊥CD,从而CD⊥平面ABB1A1,进而CD⊥B1D,CD⊥AB,∠B1DB为二面角B1-CD-B的平面角,由此能求出二面角B1-CD-B的平面角的大小.
解答 (本小题10分)
证明:(1)在直三棱柱ABC-A1B1C1中,
设BC1∩B1C=E,则E为BC1的中点,连接ED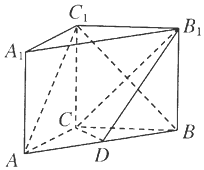
∵D为AB的中点,∴ED∥AC…..(3分)
又∵ED?平面CDB1,AC1?平面CDB1,
∴AC1∥平面CDB1. …(5分)
解:(2)∵△ABC中,AC=BC,D为AB中点,∴CD⊥AB,
又∵BB1⊥平面ABC,CD?平面ABC,∴BB1⊥CD,
又AB∩BB1=B,∴CD⊥平面ABB1A1,…(7分)
∵B1D?平面ABB1A1,AB?平面ABB1A1
∴CD⊥B1D,CD⊥AB,
∴∠B1DB为二面角B1-CD-B的平面角…(8分)
∵三角形ABC中,AB=2,∴BD=1,
在Rt△B1BD中,$tan∠{B_1}BD=\frac{{{B_1}B}}{BD}=1$,
∴∠B1BD=45°,
∴二面角B1-CD-B的平面角的大小为45°.…(10分)
点评 本题考查线面平行的证明,考查二面角的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.设α,β为不重合的平面,m,n为不重合的直线,则下列命题正确的是( )
| A. | 若m∥α,n∥β,m⊥n,则α⊥β | B. | 若m∥n,n∥α,α∥β,则m∥β | ||
| C. | α∥β,m⊥α,n∥β⇒m⊥n | D. | 若α⊥β,α∩β=n,m⊥n,则m⊥α |
6.已知圆C1:x2+y2=4与圆C2:(x-1)2+(y-3)2=4,过动点P(a,b)分别作圆C1、圆C2的切线PM,PN,(M,N分别为切点),若|PM|=|PN|,则a2+b2-6a-4b+13的最小值是( )
| A. | 5 | B. | $\frac{8}{5}$ | C. | $\frac{2}{5}\sqrt{10}$ | D. | $\frac{1}{3}$ |
3.函数y=f(x)导函数f'(x)的图象如图所示,则下列说法正确的是( )


| A. | 函数y=f(x)在(-∞,0)上单调递增 | B. | 函数y=f(x)的递减区间为(3,5) | ||
| C. | 函数y=f(x)在x=0处取得极大值 | D. | 函数y=f(x)在x=5处取得极小值 |
20.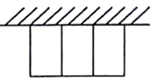 有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
 有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )
有一批材料可以建成80m的围墙,若用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的小矩形(如图所示),且围墙厚度不计,则围成的矩形的最大面积为( )| A. | 200m2 | B. | 360m2 | C. | 400m2 | D. | 480m2 |