题目内容
已知函数f(x)在R上满足
=0(λ≠0),且对任意的实数x1≠x2(x1>0,x2>0)时,有
>0成立,如果实数t满足f(lnt)-f(1)≤f(1)-f(ln
),那么t的取值范围是 .
| f(x)-f(-x) |
| 2λ |
| f(x1)-f(x2) |
| x1-x2 |
| 1 |
| t |
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据已知条件容易判断出f(x)是偶函数,且在(0,+∞)上为增函数,再根据对数的运算,从而可得到f(lnt)≤f(1),根据f(x)的奇偶性及单调性即可得到|lnt|≤1,从而根据对数函数的单调性解出该不等式即可.
解答:
解:根据已知条件及偶函数,增函数的定义可知:
f(x)是偶函数,在(0,+∞)上是增函数;
∴由f(lnt)-f(1)≤f(1)-f(ln
)得:f(lnt)≤f(1);
∴|lnt|≤1,-1≤lnt≤1;
∴
≤t≤e;
∴t的取值范围为[
,e].
故答案为:[
,e].
f(x)是偶函数,在(0,+∞)上是增函数;
∴由f(lnt)-f(1)≤f(1)-f(ln
| 1 |
| t |
∴|lnt|≤1,-1≤lnt≤1;
∴
| 1 |
| e |
∴t的取值范围为[
| 1 |
| e |
故答案为:[
| 1 |
| e |
点评:考查偶函数,增函数的定义,以及对数的运算,偶函数、增函数的运用,根据对数函数的单调性解不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )
高三年上学期期末考试中,某班级数学成绩的频率分布直方图如图所示,数据分组依次如下:[70,90),[90,110),[100,130),[130,150),估计该班级数学成绩的平均分等于( )| A、112 | B、114 |
| C、116 | D、120 |
下列函数f(x)中,满足“对任意x1,x2∈(-∞,0),当x1<x2时,都有f(x1)<f(x2)”的函数是( )
| A、f(x)=-x+1 |
| B、f(x)=x2-1 |
| C、f(x)=2x |
| D、f(x)=ln(-x) |
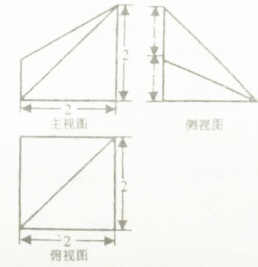
已知某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||||
| B、8 | ||||
C、
| ||||
D、
|
下列函数中是偶函数的是( )
| A、y=sinx |
| B、y=tanx |
| C、y=cosx |
| D、y=cos(x-1) |
 如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.
如图,在四棱锥ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2,BC=CD=1,顶角D1在底面ABCD内的射影恰好为点C.