题目内容
定义:分子为1且分母为正整数的分数叫做单位分数.我们可以把1拆分为无穷多个不同的单位分数之和.例如:1=
+
+
,1=
+
+
+
,1=
+
+
+
+
,…依此方法可得:1=
+
+
+
+
+
+
+
+
+
+
+
+
,其中m,n∈N*,则m+n= .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 30 |
| 1 |
| 42 |
| 1 |
| 56 |
| 1 |
| 72 |
| 1 |
| 90 |
| 1 |
| 110 |
| 1 |
| 132 |
| 1 |
| 156 |
考点:归纳推理
专题:推理和证明
分析:根据1=
+
+
+
+
+
+
+
+
+
+
+
+
,结合裂项相消法,可得
+
=
=
,解得m,n值,可得答案.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 30 |
| 1 |
| 42 |
| 1 |
| 56 |
| 1 |
| 72 |
| 1 |
| 90 |
| 1 |
| 110 |
| 1 |
| 132 |
| 1 |
| 156 |
| 1 |
| m |
| 1 |
| n |
| m+n |
| mn |
| 33 |
| 260 |
解答:
解:∵1=
+
+
+
+
+
+
+
+
+
+
+
+
,
∵2=1×2,
6=2×3,
30=5×6,
42=6×7,
56=7×8,
72=8×9,
90=9×10,
110=10×11,
132=11×12,
∴1=
+
+
+
+
+
+
+
+
+
+
+
+
=(1-
)+
+
+(
-
)+
,
+
=
=
-
+
-
=
,
∴m=20,n=13,
∴m+n=33,
故答案为:33
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 30 |
| 1 |
| 42 |
| 1 |
| 56 |
| 1 |
| 72 |
| 1 |
| 90 |
| 1 |
| 110 |
| 1 |
| 132 |
| 1 |
| 156 |
∵2=1×2,
6=2×3,
30=5×6,
42=6×7,
56=7×8,
72=8×9,
90=9×10,
110=10×11,
132=11×12,
∴1=
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 30 |
| 1 |
| 42 |
| 1 |
| 56 |
| 1 |
| 72 |
| 1 |
| 90 |
| 1 |
| 110 |
| 1 |
| 132 |
| 1 |
| 156 |
| 1 |
| 4 |
| 1 |
| m |
| 1 |
| n |
| 1 |
| 5 |
| 1 |
| 12 |
| 1 |
| 156 |
| 1 |
| m |
| 1 |
| n |
| m+n |
| mn |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 12 |
| 1 |
| 156 |
| 33 |
| 260 |
∴m=20,n=13,
∴m+n=33,
故答案为:33
点评:本题考查的知识点是归纳推理,但本题运算强度较大,属于难题.

练习册系列答案
相关题目
如图,如果输入a=3,那么输出的n值为( )


| A、2 | B、4 | C、3 | D、5 |
如图所示是一个几何体的三视图,则该几何体的表面积为( )


A、4+2
| ||
B、2+
| ||
C、2+2
| ||
D、4+
|
命题“对任意实数x∈[1,2],关于x的不等式x2-a≤0恒成立”为真命题的一个必要不充分条件是( )
| A、a≥4 | B、a≤4 |
| C、a≥3 | D、a≤3 |
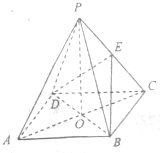 如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证:
如图,ABCD是正方形,O是该正方形的中心,P是平面ABCD外一点,PO⊥底面ABCD,E是PC的中点.求证: