题目内容

在ABC中，内角∠A，∠B，∠C的对边分别为a，b，c，若a=3，b=4，c=6，则
AB
•
AC
+
BA
•
BC
+
CA
•
CB
=
 
．
考点：平面向量数量积的运算
专题：计算题,解三角形,平面向量及应用
分析：运用向量的数量积的定义，结合三角形的余弦定理，化简整理，代入数据计算即可得到结果．
解答： 解：
AB
•
AC
+
BA
•
BC
+
CA
•
CB
=bccosA+accosB+abcosC
=
1
2
（b2+c2-a2）+
1
2
（a2+c2-b2）+
1
2
（a2+b2-c2）
=
1
2
（a2+b2+c2）=
1
2
×（32+42+62）=
61
2
．
故答案为：
61
2
．
点评：本题考查向量的数量积的定义和三角形的余弦定理，考查运算能力，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=sin2x+sin2x+3cos2x，求
（Ⅰ）函数f（x）的最小值及此时的x的集合；
（Ⅱ）函数f（x）的单调递减区间．
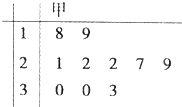某篮球运动员甲参加了10场比赛，他每场比赛得分的茎叶图如图所示，
则数据落在区间[22，30）内的概率为（　　）
A、0.6B、0.5
C、0.4D、0.3
已知：x，y为正实数，求证：
1
x
+
1
y
≥
4
x+y
．
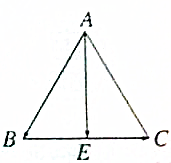如图，已知△ABC是等边三角形．
（1）求向量
AB
与向量
BC
的夹角；
（2）若E为BC的中点，求向量
AE
与
EC
的夹角．
若函数f（x）=
2x，(x＞1)
ax+1，(x≤1)
为增函数，则a的取值范围是
 
．
给出以下命题：
①若函数y=2cos（ax-
π
3
）的最小正周期是4π，则a=
1
2
；
②函数y=
sin2x-sinx
sinx-1
是奇函数；
③函数y=sinx+sin|x|的值域是[0，2]；
④当a＞1，n＞0时，总存在x0，当x＞x0时，就有logax＜xn＜ax．
其中正确命题个数为
 
．
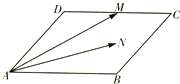如图，菱形ABCD的边长为2，∠BAD=60°，M为CD的中点，若N为菱形内任意一点（含边界），且|MN|≤1，则
AM
•
AN
的取值范围为
 
．
设全集为R，集合A={x|x2-16＜0}，B={x|
x-6
x+1
＜0}，则A∩（∁RB）=（　　）
A、（-4，0）
B、（-4，-1）
C、（-4，-1]
D、[-4，-1]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网