题目内容
已知函数f(x)=ax+x2-xlna(a>1)
(Ⅰ)若函数y=|f(x)-b+
|-3有四个零点,求b的取值范围;
(Ⅱ)若对于任意的x1,x2∈[-1,1]时,都有|f(x1)-f(x2)|≤e2-2(其中e是自然对数的底数)恒成立,求a的取值范围.
(Ⅰ)若函数y=|f(x)-b+
| 1 |
| b |
(Ⅱ)若对于任意的x1,x2∈[-1,1]时,都有|f(x1)-f(x2)|≤e2-2(其中e是自然对数的底数)恒成立,求a的取值范围.
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:导数的综合应用
分析:(I)求导函数,即可得函数f(x)在(0,+∞)上单调递增.先判断函数f(x)的极小值,再由函数有四个零点,进行等价转化方程有解问题,去掉绝对值,变成两个方程,即可解出b的范围;
(Ⅱ)|f(x1)-f(x2)|≤e2-2等价于求出函数在[-1,1]上的最大值和最小值即可求出a的取值范围.
(Ⅱ)|f(x1)-f(x2)|≤e2-2等价于求出函数在[-1,1]上的最大值和最小值即可求出a的取值范围.
解答:
解:(I)∵f(x)=ax+x2-xlna(a>1).
∴求导函数,可得f′(x)=axlna+2x-lna=2x+(ax-1)lna,
由于a>1,
∴lna>0,当x>0时,ax-1>0,
∴f′(x)>0,故函数f(x)在(0,+∞)上单调递增.
∴f(x)min=f(0)=1,
由|f(x)-b+
|-3=0,
得:f(x)=b-
+3,或f(x)=b-
-3,
∵函数y=|f(x)-b+
|-3有四个零点,
∴
,
∴b-
>4,
解得:b>2+
,2-
<b<0,
∴b的范围是(2-
,0)∪(2+
,+∞),
(Ⅱ)若对于任意的x1,x2∈[-1,1]时,
由(Ⅰ)知,f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴f(x)的最小值为f(0)=1,
总而再来比较f(-1),与f(1)的大小即可,
f(-1)=
+1+lna,f(1)=a+1-lna,
则f(1)-f(-1)=a-
-2lna,
设g(a)=a-
-2lna,(a>1),
则g′(a)=(
-1)2>0,
即g(a)在[1,+∞)上单调递增,
∴g(a)>g(1)=1-1=0,
则g(a)>0,
则f(1)>f(-1),
则f(1)是函数f(x)的最大值,即f(1)=a+1-lna,
故对?x1,x2∈[-1,1],|f(x1)-f(x2)|≤|f(1)-f(0)|=a-lna,
∴等价为a-lna≤e2-2,
令h(x)=x-lnx(x>1),
h′(x)=1-
>0,
∴h(x)在(1,+∞)上单调递增,
又a>1,∴h(a)=a-lna≤e2-2=h(e2)
解得a≤e2;
∴a的范围是(1,e2).
∴求导函数,可得f′(x)=axlna+2x-lna=2x+(ax-1)lna,
由于a>1,
∴lna>0,当x>0时,ax-1>0,
∴f′(x)>0,故函数f(x)在(0,+∞)上单调递增.
∴f(x)min=f(0)=1,
由|f(x)-b+
| 1 |
| b |
得:f(x)=b-
| 1 |
| b |
| 1 |
| b |
∵函数y=|f(x)-b+
| 1 |
| b |
∴
|
∴b-
| 1 |
| b |
解得:b>2+
| 5 |
| 5 |
∴b的范围是(2-
| 5 |
| 5 |
(Ⅱ)若对于任意的x1,x2∈[-1,1]时,
由(Ⅰ)知,f(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增,
∴f(x)的最小值为f(0)=1,
总而再来比较f(-1),与f(1)的大小即可,
f(-1)=
| 1 |
| a |
则f(1)-f(-1)=a-
| 1 |
| a |
设g(a)=a-
| 1 |
| a |
则g′(a)=(
| 1 |
| a |
即g(a)在[1,+∞)上单调递增,
∴g(a)>g(1)=1-1=0,
则g(a)>0,
则f(1)>f(-1),
则f(1)是函数f(x)的最大值,即f(1)=a+1-lna,
故对?x1,x2∈[-1,1],|f(x1)-f(x2)|≤|f(1)-f(0)|=a-lna,
∴等价为a-lna≤e2-2,
令h(x)=x-lnx(x>1),
h′(x)=1-
| 1 |
| x |
∴h(x)在(1,+∞)上单调递增,
又a>1,∴h(a)=a-lna≤e2-2=h(e2)
解得a≤e2;
∴a的范围是(1,e2).
点评:本题考查导数知识的运用,考查函数的单调性,考查函数的零点,考查恒成立问题,考查学生分析解决问题的能力,解题的关键是利用导数确定函数的最值.

练习册系列答案
相关题目
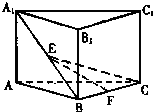 如图,三棱柱ABC-A1B1 C1中,侧棱AA1⊥平面ABC,AB=BC=AA1=2,AC=2
如图,三棱柱ABC-A1B1 C1中,侧棱AA1⊥平面ABC,AB=BC=AA1=2,AC=2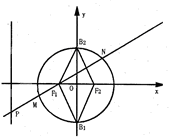 如图,椭圆C:
如图,椭圆C: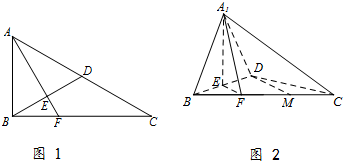
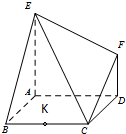 如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=
如图,已知多面体EABCDF的底面ABCD是边长为2的正方形,EA⊥底面ABCD,FD∥EA,且FD=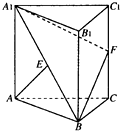 如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,三棱柱ABC-A1B1C1的侧棱AA1⊥平面ABC,△ABC为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.