题目内容
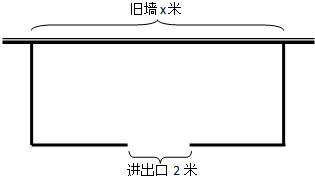
围建一个面积为360平方米的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2米的进出口,如图所示,已知旧墙的维修费用为45元/米,新墙的造价为180元/米,设利用的旧墙的长度为x米,工程总造价为y(单位:元).
(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.

(Ⅰ)将y表示为x的函数;
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
考点:根据实际问题选择函数类型
专题:函数的性质及应用
分析:(Ⅰ)设矩形的另一边长为a米,列出函数的表达式,注明定义域.
(II)利用基本不等式直接求解最值即可.
(II)利用基本不等式直接求解最值即可.
解答:
解:(Ⅰ)设矩形的另一边长为a米,
则y=45x+180(x-2)+180×2a=225x+360a-360(2分)
由已知xa=360,得a=
,(4分)
所以y=225x+
-360(x>0)(6分)
(II)∵x>0,∴225x+
≥2
=10800∴y=225x+
-360≥10400(9分)
当且仅当225x=
,即x=24时,等号成立.(11分)
所以当x=24米时,修建围墙的总费用最小,最小总费用是10440元. (12分)
则y=45x+180(x-2)+180×2a=225x+360a-360(2分)
由已知xa=360,得a=
| 360 |
| x |
所以y=225x+
| 3602 |
| x |
(II)∵x>0,∴225x+
| 3602 |
| x |
225x•
|
| 3602 |
| x |
当且仅当225x=
| 3602 |
| x |
所以当x=24米时,修建围墙的总费用最小,最小总费用是10440元. (12分)
点评:本题考查函数与方程的综合应用,列出函数的解析式是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知2∈{1,a,a-1},则实数a的值为( )
| A、2 | B、3 | C、2或3 | D、无解 |
若非零向量
,
使得|
+
|=|
|-|
|成立的一个充分非必要条件是( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
已知全集U=R,集合A={x|y=
},B={x|
<2x<4},则(∁UA)∩B等于( )
| x |
| 1 |
| 2 |
| A、{x|-1<x<2} |
| B、{x|-1<x<0} |
| C、{x|x<1} |
| D、{x|-2<x<0} |
阅读程序框图,运行相应的程序,输出的结果为( )
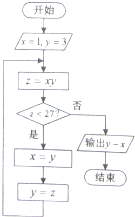

| A、6 | B、-6 | C、0 | D、18 |
已知复数z满足(1-i)z=2,则|
|为( )
. |
| z |
| A、1+i | ||
| B、1-i | ||
C、
| ||
| D、2 |
化(
) -
的结果是( )
| 27 |
| 125 |
| 1 |
| 3 |
| A、3 | ||
| B、5 | ||
C、
| ||
D、
|