题目内容
化简:(1)
-
= ;
(2)sin(
+α)sin(
-α)= .
| 1 |
| 1-tanθ |
| 1 |
| 1+tanθ |
(2)sin(
| π |
| 4 |
| π |
| 4 |
考点:两角和与差的正弦函数
专题:三角函数的求值
分析:(1)通分合并后,由二倍角的正切公式可得;(2)原式=sin(
+α)sin[
-(
+α)]=sin(
+α)cos(
+α),由二倍角的正弦公式可得.
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
解答:
解:(1)原式=
-
=
=
=tan2θ
(2)原式=sin(
+α)sin[
-(
+α)]
=sin(
+α)cos(
+α)
=
•2sin(
+α)cos(
+α)
=
sin2(
+α)
=
sin(
+2α)
=
cos2α
故答案为:tan2θ,
cos2α
| 1+tanθ |
| (1-tanθ)(1+tanθ) |
| 1-tanθ |
| (1+tanθ)(1-tanθ) |
=
| 1+tanθ-1+tanθ |
| (1-tanθ)(1+tanθ) |
| 2tanθ |
| 1-tan2θ |
(2)原式=sin(
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
=sin(
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
=
| 1 |
| 2 |
| π |
| 4 |
=
| 1 |
| 2 |
| π |
| 2 |
=
| 1 |
| 2 |
故答案为:tan2θ,
| 1 |
| 2 |
点评:本题考查两角和与差的三角函数公式,涉及诱导公式的应用,属中档题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
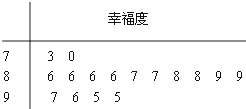 前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):
前不久,省社科院发布了2013年度“安徽城市居民幸福排行榜”,芜湖市成为本年度安徽最“幸福城”.随后,师大附中学生会组织部分同学,用“10分制”随机调查“阳光”社区人们的幸福度.现从调查人群中随机抽取16名,如图所示的茎叶图记录了他们的幸福度分数(以小数点前的一位数字为茎,小数点后的一位数字为叶):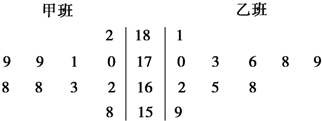
 函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为
函数y=Asin(ωx+ϕ)在一个周期内的图象如图,则此函数的解析式为