题目内容
数列{an}满足a1=1,a2=3,且an+2=(1+2|cos
|)an+|sin
|,(n∈N+)
(1)证明:数列{a2k}(k∈N+)为等比数列;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和.
| nπ |
| 2 |
| nπ |
| 2 |
(1)证明:数列{a2k}(k∈N+)为等比数列;
(2)求数列{an}的通项公式;
(3)求数列{an}的前n项和.
考点:数列的求和,等比关系的确定
专题:等差数列与等比数列
分析:(1)设n=2k,k∈N*,由已知条件推导出
=3,由此能证明数列{a2k}为等比数列.
(2)设n=2k-1,由已知条件推导出a2k+1-a2k-1=1,从而得到a2k-1=k.由此能求出an .
(3)设数列{an}的前n项和为Tn ,利用分类讨论思想和分组求和法能求出数列{an}的前n项和.
| a2k+2 |
| a2k |
(2)设n=2k-1,由已知条件推导出a2k+1-a2k-1=1,从而得到a2k-1=k.由此能求出an .
(3)设数列{an}的前n项和为Tn ,利用分类讨论思想和分组求和法能求出数列{an}的前n项和.
解答:
(1)证明:设n=2k,k∈N*,
∵an+2=(1+2|cos
|)an+|sin
|,(n∈N+),
又a2=3,
∴
=3.
∴当k∈N*时,数列{a2k}为等比数列.
∴a2k=a2•3k-1=3k.
(2)解:设n=2k-1,k∈N*.
由a2k+1=(1+2|cos
|)a2k-1+|sin
|=a2k-1+1,
∴a2k+1-a2k-1=1.
∴当k∈N*时,数列{a2k-1}为等差数列.
∴a2k-1=a1+(k-1)•1=k.
∴an =
.
(3)解:设数列{an}的前n项和为Tn .
由(2)知:
当n为奇数时,Tn=a1 +a2+a3+…+an-1+an
=1+3+2+32+3+33+4+34+…+3
+
=(1+2+3+4+…+
)+(3+32+33+34+…+3
)
=
+
=
(1+
)+
(3
-1).
当n为偶数时,Tn=a1 +a2+a3+…+an-1+an
=1+3+2+32+3+33+4+34+…+
+3
=(1+2+3+4+…+
)+(3+32+33+34+…+3
)
=
+
=
+
(3
-1).
∵an+2=(1+2|cos
| nπ |
| 2 |
| nπ |
| 2 |
又a2=3,
∴
| a2k+2 |
| a2k |
∴当k∈N*时,数列{a2k}为等比数列.
∴a2k=a2•3k-1=3k.
(2)解:设n=2k-1,k∈N*.
由a2k+1=(1+2|cos
| (2k-1)π |
| 2 |
| (2k-1)π |
| 2 |
∴a2k+1-a2k-1=1.
∴当k∈N*时,数列{a2k-1}为等差数列.
∴a2k-1=a1+(k-1)•1=k.
∴an =
|
(3)解:设数列{an}的前n项和为Tn .
由(2)知:
当n为奇数时,Tn=a1 +a2+a3+…+an-1+an
=1+3+2+32+3+33+4+34+…+3
| n-1 |
| 2 |
| n+1 |
| 2 |
=(1+2+3+4+…+
| n+1 |
| 2 |
| n-1 |
| 2 |
=
| ||||
| 2 |
3(1-3
| ||
| 1-3 |
=
| n+1 |
| 4 |
| n+1 |
| 2 |
| 3 |
| 2 |
| n-1 |
| 2 |
当n为偶数时,Tn=a1 +a2+a3+…+an-1+an
=1+3+2+32+3+33+4+34+…+
| n-1 |
| 2 |
| n |
| 2 |
=(1+2+3+4+…+
| n-1 |
| 2 |
| n |
| 2 |
=
| ||||
| 2 |
3(1-3
| ||
| 1-3 |
=
| n2-1 |
| 4 |
| 3 |
| 2 |
| n |
| 2 |
点评:本题考查等比数列的证明,考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
已知点M在双曲线
-
=1上,它到左准线的距离为2,则它到左焦点的距离为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、7 | ||
| B、3 | ||
C、
| ||
D、
|
 已知椭圆
已知椭圆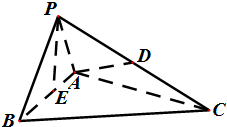 如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC=
如图,四面体P-ABC中,△PAB为边长为1的等边三角形,△PBC与△PAC均为斜边为PC的直角三角形,且PC= 如图,已知PA⊥面ABCD,PA=AB=AD=
如图,已知PA⊥面ABCD,PA=AB=AD=