题目内容
已知数列{an}为等差数列,则有
a1-2a2+a3=0,
a1-3a2+3a3-a4=0,
a1-4a2+6a3-4a4+a5=0
写出第四行的结论 .
a1-2a2+a3=0,
a1-3a2+3a3-a4=0,
a1-4a2+6a3-4a4+a5=0
写出第四行的结论
考点:二项式系数的性质,等差数列的性质
专题:等差数列与等比数列
分析:观察已知的三个等式,找出规律,写出第四个等式即可.
解答:
解:数列{an}为等差数列,则有
a1-2a2+a3=0,
a1-3a2+3a3-a4=0,
a1-4a2+6a3-4a4+a5=0,
三个式子的项数分别是3,4,5,所以第四个式子有6项.并且奇数项为正,偶数项为负,项的系数满足二项式定理系数的形式.
所以第四行的结论:a1-5a2+10a3-10a4+5a5-a6=0.
故答案为:a1-5a2+10a3-10a4+5a5-a6=0.
a1-2a2+a3=0,
a1-3a2+3a3-a4=0,
a1-4a2+6a3-4a4+a5=0,
三个式子的项数分别是3,4,5,所以第四个式子有6项.并且奇数项为正,偶数项为负,项的系数满足二项式定理系数的形式.
所以第四行的结论:a1-5a2+10a3-10a4+5a5-a6=0.
故答案为:a1-5a2+10a3-10a4+5a5-a6=0.
点评:本题考查数列的性质,归纳推理的应用,二项式定理的应用.

练习册系列答案
相关题目
甲乙两个班级进行计算机考试,按照学生考试成绩优秀和不优秀统计后,得到如下的列联表:
利用独立性检验估计,你认为成绩与班级( )
| 优秀 | 不优秀 | 总计 | |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 总计 | 17 | 73 | 90 |
| A、有95%的把握有关 |
| B、无关 |
| C、有99%的把握有关 |
| D、无法确定 |
如图是某程序框图,若执行后输出y的值为0,则输入x的值不能是( )


| A、0 | ||
B、
| ||
| C、2 | ||
| D、2010 |
方程2x=cosx的解的个数为( )
| A、0 | B、1 | C、2 | D、无穷多个 |
如图的框图的功能是计算表达式1+2+3+…+10的值,则在①、②两处应填入( )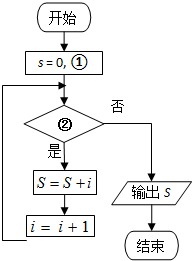

| A、i=0,i≤10 |
| B、i=0,i<10 |
| C、i=1,i≤10 |
| D、i=1,i<10 |