题目内容
9.如图,△AB1C1,△B1B2C2,△B2B3C3是三个边长为2的等边三角形,且有一条边在同一直线上,边B3C3上有5个不同的点P1,P2,P3,P4,P5,设${m_i}=\overrightarrow{A{C_2}}•\overrightarrow{A{P_i}}$(i=1,2,…,5),则m1+m2+…+m5=90.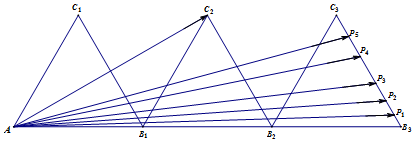
分析 建立坐标系,求出直线B3C3的方程,得出Pi的坐标的关系,代入数量积公式计算即可.
解答 解:以A为原点,以AB3所在直线为x轴建立平面直角坐标系,如图所示: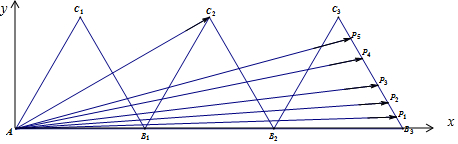
则A(0,0),C2(3,$\sqrt{3}$),B3(6,0),C3(5,$\sqrt{3}$),
∴直线B3C3所在直线方程为$y=-\sqrt{3}(x-6)$,即$\sqrt{3}$x+y-6$\sqrt{3}$=0,
设Pi(xi,yi),则$\sqrt{3}$xi+yi=6$\sqrt{3}$.
∴$\overrightarrow{A{C}_{2}}•\overrightarrow{A{P}_{i}}$=3xi+$\sqrt{3}$yi=18,
∴m1+m2+…+m5=18×5=90.
故答案为90.
点评 本题考查向量的数量积的坐标表示,注意运用直线方程,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
19.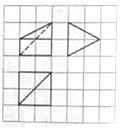 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 4 |
17.已知F1,F2为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,以F1F2为直径的圆与双曲线右支的一个交点为P,PF1与双曲线相交于点Q,且|PQ|=2|QF1|,则该双曲线的离心率为 ( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{5}}{2}$ |