题目内容
△ABC中,角A、B、C所对应的边分别为a、b、c,若
=
.
(1)求角A;
(Ⅱ)设
=(sinB,cos2B),
=(2,1),求
•
的最大值.
| a-c |
| b-c |
| sinB |
| sinA+sinC |
(1)求角A;
(Ⅱ)设
| m |
| n |
| m |
| n |
考点:余弦定理的应用,平面向量数量积的坐标表示、模、夹角
专题:计算题,三角函数的求值,解三角形,平面向量及应用
分析:(1)由正弦定理将角化为边,再由余弦定理即可求得角A;
(II)由向量的数量积的坐标表示,结合二倍角公式及三角换元,由二次函数的最值求法,即可得到最大值.
(II)由向量的数量积的坐标表示,结合二倍角公式及三角换元,由二次函数的最值求法,即可得到最大值.
解答:
解:(1)由
=
则
=
,
即a2=b2+c2-bc,
由余弦定理,a2=b2+c2-2bccosA,得
cosA=
,
由于A为锐角,
则A=
;
(II)
•
=2sinB+cos2B,
=2sinB+1-2sin2B
=-2sin2B+2sinB+1,B∈(0,
),
令t=sinB,则t∈(0,1].
则
•
=-2t2+2t+1=-2(t-
)2+
,t∈(0,1].
∴t=
时,
•
取得最大值
.
| a-c |
| b-c |
| sinB |
| sinA+sinC |
则
| a-c |
| b-c |
| b |
| a+c |
即a2=b2+c2-bc,
由余弦定理,a2=b2+c2-2bccosA,得
cosA=
| 1 |
| 2 |
由于A为锐角,
则A=
| π |
| 3 |
(II)
| m |
| n |
=2sinB+1-2sin2B
=-2sin2B+2sinB+1,B∈(0,
| 2π |
| 3 |
令t=sinB,则t∈(0,1].
则
| m |
| n |
| 1 |
| 2 |
| 3 |
| 2 |
∴t=
| 1 |
| 2 |
| m |
| n |
| 3 |
| 2 |
点评:本题考查正弦定理和余弦定理的运用,考查平面向量的数量积的坐标表示,考查三角函数的求值,考查二次函数的值域问题,考查运算能力,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
函数f(x)=alg(3-ax),a>0,a≠1在定义域[-1,1]上是减函数,则实数a的取值范围是( )
| A、(1,3) |
| B、(1,+∞) |
| C、(3,+∞) |
| D、(0,1) |
已知f(x)=sin2x+|sin2x|(x∈R),则下列判断正确的是( )
| A、f(x)是周期为2π的奇函数 |
| B、f(x)是值域为[0,2]周期为π的函数 |
| C、f(x)是周期为2π的偶函数 |
| D、f(x)是值域为[0,1]周期为π的函数 |
已知集合A={1,2},B={1},则“x∈A”是“x∈B”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
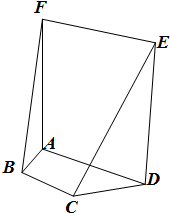 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=2