题目内容
4.在同一平面直角坐标系中经过伸缩变换$\left\{\begin{array}{l}x'=5x\\ y'=3y\end{array}\right.$后,曲线C变为曲线2x′2+8y′2=1,则曲线C的方程为( )| A. | 25x2+36y2=1 | B. | 50x2+72y2=1 | C. | 10x2+24y2=1 | D. | $\frac{{2{x^2}}}{25}+\frac{{8{y^2}}}{9}=1$ |
分析 把$\left\{\begin{array}{l}x'=5x\\ y'=3y\end{array}\right.$代入曲线2x′2+8y′2=1,即可得出.
解答 解:把$\left\{\begin{array}{l}x'=5x\\ y'=3y\end{array}\right.$代入曲线2x′2+8y′2=1,可得2(5x)2+8(3y)2=1,化为50x2+72y2=1,即为曲线C的方程.
故选:B.
点评 本题考查了曲线的变换公式的应用,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知等差数列{an}满足a1+a2=-1,a3=4,则a4+a5=( )
| A. | 17 | B. | 16 | C. | 15 | D. | 14 |
19.执行如图所示的程序框图,输出的y值为( )
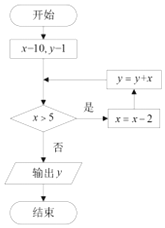

| A. | 15 | B. | 17 | C. | 19 | D. | 21 |
9.一个三棱锥的三视图如图(图中小正方形的边长为1),则这个三棱锥的体积是( )
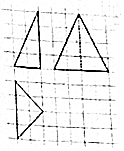

| A. | $\frac{32}{3}$ | B. | 8 | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
16.定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$,则符合条件$|{\begin{array}{l}z&{1+i}\\{-i}&{2i}\end{array}}|=0$的复数z的共轭复数$\overline z$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.通过$\widehat{{e}_{1}}$,$\widehat{{e}_{2}}$,…,$\widehat{{e}_{n}}$来判断模拟型拟合的效果,判断原始数据中是否存在可疑数据,这种分工称为( )
| A. | 回归分析 | B. | 独立性检验分析 | C. | 残差分析 | D. | 散点图分析 |
14.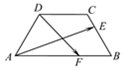 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
 如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )
如图,等腰梯形ABCD中,AB=4,BC=CD=2,若E、F分别是边BC、AB上的点,且满足$\frac{BE}{BC}$=$\frac{AF}{AB}$=λ,当$\overrightarrow{AE}$•$\overrightarrow{DF}$=0时,则有( )| A. | λ∈($\frac{1}{8}$,$\frac{1}{4}$) | B. | λ∈($\frac{1}{4}$,$\frac{3}{8}$) | C. | λ∈($\frac{3}{8}$,$\frac{1}{2}$) | D. | λ∈($\frac{1}{2}$,$\frac{5}{8}$) |