题目内容
已知函数f(x)=x3+ax2+bx+4(x∈R)在x=2处取得极小值.
(1)若函数f(x)的极小值是-4,求f(x);
(2)若函数f(x)的极小值不小于-6,问:是否存在实数k与函数f(x),使得函数f(x)在[k,k+3]上单调递减.若存在,求出k的取值集合与f(x);若不存在,说明理由.
解:(1)f′(x)=3x2+2ax+b,
由 解得
解得 检验可知,满足题意,
检验可知,满足题意,
故f(x)=x3-2x2-4x+4(x∈R).
(2)假设存在实数k,使得函数f(x)在[k,k+3]上单调递减.
设f′(x)=3x2+2ax+b=0的两根为x1,x2(x1<x2),则x2=2.由f′(x)<0,得x∈(x1,x2),∴f(x)的单调递减区间为[x1,x2].
由x1+2=- ,解得x1=-
,解得x1=- -2,∴f(x)的单调递减区间为
-2,∴f(x)的单调递减区间为
由条件有
∴函数f(x)在[-1,2]上单调递减.
 k=-1,
k=-1,
∴存在实数k=-1,满足题意.
∴k的取值集合是{-1},f(x)=x3- x2-6x+4.
x2-6x+4.

练习册系列答案
相关题目
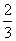 +4(a,b∈R),若f
+4(a,b∈R),若f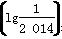 =2 013,则f(lg 2 014)=( )
=2 013,则f(lg 2 014)=( )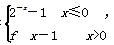 若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围为( )
若方程f(x)=x+a有且只有两个不相等的实数根,则实数a的取值范围为( )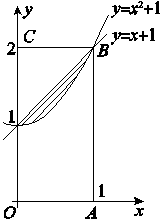
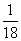 B.
B.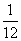 C.
C.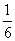 D.
D.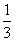



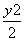 -x2=1的渐近线方程为y=±
-x2=1的渐近线方程为y=±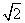 x;
x;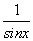 ≥2”是真命题;
≥2”是真命题;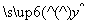 =3+2x,当变量x增加2个单位,其预报值平均增加4个单位;
=3+2x,当变量x增加2个单位,其预报值平均增加4个单位;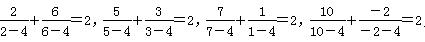 依照以上各式的规律,得到一般性的等式为
依照以上各式的规律,得到一般性的等式为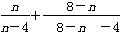 =2(n≠4).
=2(n≠4).