题目内容
设函数f(x)满足f(x)=f(3x),且当x∈[1,3)时,f(x)=lnx.若在区间[1,9)内,存在3个不同的实数x1,x2,x3,使得
=
=
=t,则实数t的取值范围为 .
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(x3) |
| x3 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:可以根据函数f(x)满足f(x)=f(3x),求出x∈[3,9)上的解析式,在区间[1,9)内,函数g(x)=f(x)-tx有三个不同零点,可转化成“f(x)-tx=0在区间[1,9)上有三个解,利用数形结合,即可求出所求.
解答:
解:设x∈[3,9),则
∈[1,3),
∵x∈[1,3),f(x)=lnx,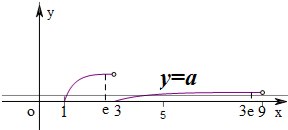
∴f(
)=ln
,
∵函数f(x)满足f(x)=f(3x),
∴f(x)=
,
∵在区间[1,9)内,存在3个不同的实数x1,x2,x3,使得
=
=
=t,
∴f(x)-tx=0在区间[1,9)上有三个解,
则y=t与h(x)=
的图象有三个交点,
当x∈[1,3),h(x)=
=
,则h′(x)=
=0,解得x=e,
∴当x∈[1,e)时,h′(x)>0,
当x∈(e,3)时,h′(x)<0即函数h(x)=
在[1,e)上单调递增,在(e,3)上单调递减,
∴当x=e处,函数h(x)=
在[1,3)上取最大值是
,
当x∈[3,9),h(x)=
=
,则h′(x)=
=0,解得x=3e,
∴当x∈[3,3e)时,h′(x)>0,当x∈(3e,9)时,h′(x)<0,
即函数h(x)=
在[3,3e)上单调递增,在(3e,9)上单调递减,
∴当x=3e处,函数h(x)=
在[3,9)上取最大值
,
根据函数的单调性,以及h(1)=0,h(e)=
,h(3)=0,h(3e)=
,h(9)=
,画出函数的图象,
根据图象可知y=t与h(x)在[1,3)上一个交点,在[3,3e) 上两个交点,
∴在区间[1,9)内,函数g(x)=f(x)-tx有三个不同零点,则实数a的取值范围是(
,
).
故答案为:(
,
)
| x |
| 3 |
∵x∈[1,3),f(x)=lnx,

∴f(
| x |
| 3 |
| x |
| 3 |
∵函数f(x)满足f(x)=f(3x),
∴f(x)=
|
∵在区间[1,9)内,存在3个不同的实数x1,x2,x3,使得
| f(x1) |
| x1 |
| f(x2) |
| x2 |
| f(x3) |
| x3 |
∴f(x)-tx=0在区间[1,9)上有三个解,
则y=t与h(x)=
| f(x) |
| x |
当x∈[1,3),h(x)=
| f(x) |
| x |
| lnx |
| x |
| 1-lnx |
| x2 |
∴当x∈[1,e)时,h′(x)>0,
当x∈(e,3)时,h′(x)<0即函数h(x)=
| f(x) |
| x |
∴当x=e处,函数h(x)=
| f(x) |
| x |
| 1 |
| e |
当x∈[3,9),h(x)=
| f(x) |
| x |
ln
| ||
| x |
1-ln
| ||
| x2 |
∴当x∈[3,3e)时,h′(x)>0,当x∈(3e,9)时,h′(x)<0,
即函数h(x)=
ln
| ||
| x |
∴当x=3e处,函数h(x)=
ln
| ||
| x |
| 1 |
| 3e |
根据函数的单调性,以及h(1)=0,h(e)=
| 1 |
| e |
| 1 |
| 3e |
| ln3 |
| 9 |
根据图象可知y=t与h(x)在[1,3)上一个交点,在[3,3e) 上两个交点,
∴在区间[1,9)内,函数g(x)=f(x)-tx有三个不同零点,则实数a的取值范围是(
| ln3 |
| 9 |
| 1 |
| 3e |
故答案为:(
| ln3 |
| 9 |
| 1 |
| 3e |
点评:本题主要考查函数的零点与方程的根的关系,同时考查了运算求解的能力,体现了化归与转化、数形结合的数学思想,属于难题.

练习册系列答案
相关题目