题目内容
点O在△ABC内，试证明：
•S△OBC+
•S△OAC+
•S△OAB=0．
| OA |
| OB |
| OC |
考点：正弦定理
专题：平面向量及应用
分析：连接AO，并延长BC于D，连结BO并延长交AC于E，连结CO并延长交AB与F，过A作AM∥BE交CF延长线于M，作AN∥CF交BE延长线于N，则四边形AMON为平行四边形．通过AM∥BE，推断出△AMF∽△BOF，求得边长的比例关系，进而表示出
和
，则
可表示出来，设出△AOC与△AOB高，确定S△AOB：S△BOC=AE：EB，和S△AOC：S△BOC=AF：FB，带入原式．
| AM |
| AN |
| AO |
解答：
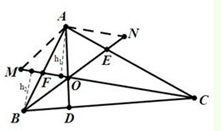证明：如图，连接AO，并延长BC于D，连结BO并延长交AC于E，连结CO并延长交AB与F，过A作AM∥BE交CF延长线于M，作AN∥CF交BE延长线于N，则四边形AMON为平行四边形．
∴
=
+
，
∵AM∥BE，
∴△AMF∽△BOF，
∴
=
，
∴
=
•
，同理
=
•
，
∴
=
•
+
•
，
∵△AOC与△AOB有公共的底边OC，设它们的相应的高分别是h1，h2，
则S△AOC：S△BOC=h1：h2=AF：FB，同理S△AOB：S△BOC=AE：EB，
=
•
+
•
，
∴
•S△BOC=S△AOC•
+S△AOB•
，
∴结论成立．
证明：如图，连接AO，并延长BC于D，连结BO并延长交AC于E，连结CO并延长交AB与F，过A作AM∥BE交CF延长线于M，作AN∥CF交BE延长线于N，则四边形AMON为平行四边形．∴
| AO |
| AM |
| AN |
∵AM∥BE，
∴△AMF∽△BOF，
∴
| AM |
| OB |
| AF |
| FB |
∴
| AM |
| AF |
| FB |
| OB |
| AN |
| AE |
| EC |
| OC |
∴
| AO |
| AF |
| FB |
| OB |
| AE |
| EC |
| OC |
∵△AOC与△AOB有公共的底边OC，设它们的相应的高分别是h1，h2，
则S△AOC：S△BOC=h1：h2=AF：FB，同理S△AOB：S△BOC=AE：EB，
| AO |
| S△AOC |
| S△BOC |
| OB |
| SAOB |
| SBOC |
| OC |
∴
| AO |
| OB |
| OC |
∴结论成立．
点评：本题主要考查了向量的计算与运用．考查了学生综合分析问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
将边长为1的正方形ABCD沿对角线BD折成直二面角，若点P满足
=
-
+
，则|
|的值为（ ）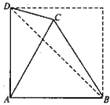
| BP |
| 1 |
| 2 |
| BA |
| 1 |
| 2 |
| BC |
| BD |
| BP |
A、
| ||||
| B、2 | ||||
C、
| ||||
D、
|
已知f（x）是奇函数，且f（x+2）=f（x），当0≤x≤1时，f（x）=2x（1-x），则f（-
）=（ ）
| 5 |
| 2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
函数f（x）=2|x|-1在区间[-1，2]的值域是（ ）
| A、[1，4] | ||
B、[
| ||
| C、[1，2] | ||
D、[
|
已知1∈{a，a+1，a2}，则实数a的可取值是（ ）
| A、0 | B、1 |
| C、-1 | D、0或1或-1 |