题目内容
已知函数f(x)=xln x.
(1)求f(x)的单调区间和极值;
(2)设A(x1,f(x1)),B(x2,f(x2)),且x1≠x2,证明: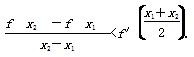
解:(1)f(x)的定义域为(0,+∞),
f′(x)=ln x+x· =1+ln x.
=1+ln x.
令f′(x)>0,则ln x>-1=ln 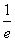 ,∴x>
,∴x>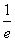 ;令f′(x)<0,则ln x<-1=ln
;令f′(x)<0,则ln x<-1=ln 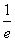 ,∴0<x<
,∴0<x<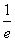 ,
,
∴f(x)的单调递增区间是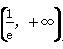 ,单调递减区间是
,单调递减区间是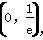 ,
,
f(x)极小值=f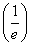 =
=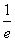 ln
ln 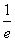 =-
=-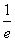 ,f(x)无极大值.
,f(x)无极大值.
(2)不防设x1<x2,
 =ln
=ln 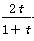 +
+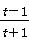
=ln 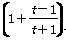 -
-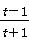 ,
,
令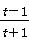 =x(x>0),h(x)=ln(1+x)-x,
=x(x>0),h(x)=ln(1+x)-x,
则h′(x)=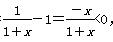 ,h(x)在(0,+∞)上单调递减,
,h(x)在(0,+∞)上单调递减,
∴h(x)<h(0)=0,
即ln (1+x)<x,即g′(t)=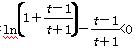 恒成立,
恒成立,
∴g(t)在(1,+∞)上是减函数,∴g(t)<g(1)=0,
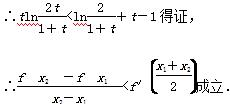

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
 的公比
的公比 ,前
,前 项和为
项和为 ,则
,则 等于( )
等于( ) D、
D、
 且
且 ,则
,则 的最小值为 ( )
的最小值为 ( ) B.
B.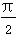 <an+1-an<π
<an+1-an<π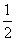 B.
B.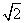 ,AF=1,M在EF上且AM∥平面BDE,则点M的坐标为( )
,AF=1,M在EF上且AM∥平面BDE,则点M的坐标为( )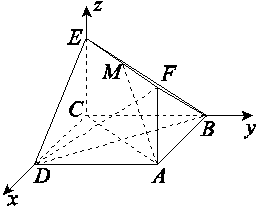
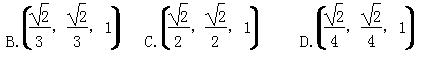
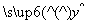 =1.23x+0.08;
=1.23x+0.08;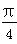 ;
;