题目内容
设直线x=t与函数f(x)=x2+1,g(x)=x+ln x的图象分别交于P,Q两点,则|PQ|的最小值是( )
A.-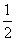 B.
B.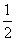 C.1 D.-
C.1 D.-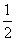 或1
或1
C
[解析] 直线x=t与函数f(x)=x2+1,g(x)=x+ln x的图象分别交于P(t,f(t)),Q(t,g(t))两点,则|PQ|=|f(t)-g(t)|.
记h(t)=f(t)-g(t)=t2+1-(t+ln t).
函数h(t)的定义域为(0,+∞),h′(t)=2t-1-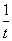 =
=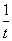 (2t2-t-1)=
(2t2-t-1)=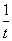 (2t+1)(t-1).
(2t+1)(t-1).
由h′(t)=0,解得t=1或t=-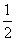 (舍去).
(舍去).
显然当t∈(0,1)时,h′(t)<0,函数h(t)单调递减;当t∈(1,+∞)时,h′(t)>0,函数h(t)单调递增.
故函数h(t)的最小值为h(1)=12+1-(1+ln 1)=1,故|PQ|的最小值为1.

练习册系列答案
相关题目
 ( )
( ) B、
B、
 D、
D、

 ;
; ; 若
; 若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围.
的取值范围.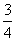 B.
B.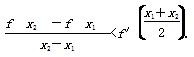


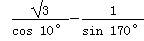 =( )
=( )