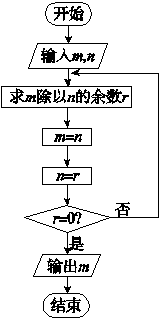
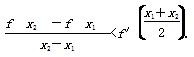题目内容
若函数f(x)=xcos x在(0,+∞)内的全部极值点按从小到大的顺序排列为a1,a2,…,an,…,则对任意正整数n必有( )
A.π<an+1-an<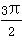 B.
B.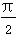 <an+1-an<π
<an+1-an<π
C.0<an+1-an<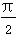 D.-
D.-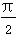 <an+1-an<0
<an+1-an<0
B
[解析] f′(x)=cos x-xsin x,令f′(x)=0,得 =tan x,函数y=
=tan x,函数y= 与y=tan x的图象如图所示,an与an+1就是两个函数图象相邻交点的横坐标.由于函数y=
与y=tan x的图象如图所示,an与an+1就是两个函数图象相邻交点的横坐标.由于函数y= 在(0,+∞)上是减函数,故随着n的增加,an越来越接近其所在周期内的零点(y=tan x的零点),故an+1-an<π,又an与an+1在各自周期内零点的右侧,因此an+1-an>
在(0,+∞)上是减函数,故随着n的增加,an越来越接近其所在周期内的零点(y=tan x的零点),故an+1-an<π,又an与an+1在各自周期内零点的右侧,因此an+1-an> ,故选B.
,故选B.


练习册系列答案
相关题目
 满足
满足 ,
, ,则
,则 ( )
( )
 ,则z=2x+y的最大值为 .
,则z=2x+y的最大值为 . ;
; ; 若
; 若 是
是 的必要非充分条件,求实数
的必要非充分条件,求实数 的取值范围.
的取值范围. ,
, 2,
2, 的大小关系是( )
的大小关系是( )