题目内容
在△ABC中,∠C=90°,AB=8,∠ABC=30°,PC⊥面ABC,PC=4,P′是AB上的一动点,则PP′的最小值为 .
考点:点、线、面间的距离计算
专题:空间位置关系与距离
分析:过点C作CD⊥AB,连接PD,由三垂线定理知,PD⊥AB,点D就是所求的P′点,所以PP′的最小值是PD.
解答:
解:过点C作CD⊥AB,连接PD,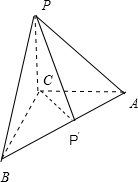
由三垂线定理知,PD⊥AB,
点D就是所求的P′点,所以PP′的最小值是PD,
因为,∠C=90°,AB=8,∠ABC=30°,PC⊥面ABC,PC=4,
所以BC=ABcosB=4
,CD=BCsinB=2
,
PD2=PC2+CD2=16+12=28,
∴PP′=PD=2
.
故答案为:2
.

由三垂线定理知,PD⊥AB,
点D就是所求的P′点,所以PP′的最小值是PD,
因为,∠C=90°,AB=8,∠ABC=30°,PC⊥面ABC,PC=4,
所以BC=ABcosB=4
| 3 |
| 3 |
PD2=PC2+CD2=16+12=28,
∴PP′=PD=2
| 7 |
故答案为:2
| 7 |
点评:本题考查线段最小值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
