题目内容
9.函数f(x)=$\sqrt{2-{2}^{x}}$+lnx的定义域为(0,1].分析 函数f(x)=$\sqrt{2-{2}^{x}}$+lnx有意义,只需2-2x≥0,x>0,解不等式即可得到所求定义域.
解答 解:函数f(x)=$\sqrt{2-{2}^{x}}$+lnx有意义,
只需2-2x≥0,x>0,
解得x≤1,且x>0,
则函数的定义域为(0,1].
故答案为:(0,1].
点评 本题考查函数的定义域的求法,注意偶次根式被开方数非负,对数真数大于0,考查运算能力,属于基础题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
4.函数f(x)=x3+lnx-2零点所在的大致区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
1.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,左焦点为F,过F作垂直于x轴的直线与双曲线相交于B、C两点,若△ABC为锐角三角形,则双曲线的离心率的取值范围为( )
| A. | (1,2) | B. | (1,$\sqrt{2}$) | C. | ($\sqrt{2}$,2) | D. | (2,+∞) |
18.已知幂函数f(x)=xα(α为常数)的图象过点$P({2,\frac{1}{2}})$,则f(x)的单调递减区间是( )
| A. | (-∞,0) | B. | (-∞,+∞) | C. | (-∞,0)∪(0,+∞) | D. | (-∞,0)与(0,+∞) |
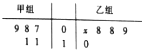 如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.
如图所示的茎叶图记录了甲、乙两组各5名同学的投篮命中次数,乙组记录中有一个数据模糊,无法确认,在图中用x表示.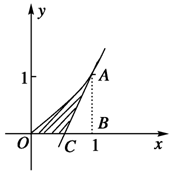 在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$,试求:
在曲线y=x2(x≥0)上某一点A处作一切线使之与曲线以及x轴所围成的面积为$\frac{1}{12}$,试求: