题目内容
若不等式m＜
，x∈[1，5]恒成立，则实数m的取值范围为 ．
| 1 |
| x |
考点：函数恒成立问题
专题：综合题
分析：构造函数，确定函数的单调性，求出函数的最值，即可求得实数m的取值范围．
解答：
解：构造函数y=
，x∈[1，5]
∴函数在区间上为单调减函数
∴x=5时，函数取得最小值
∴不等式m＜
，x∈[1，5]恒成立时，m＜
∴实数m的取值范围为（-∞，
）
故答案为：（-∞，
）
| 1 |
| x |
∴函数在区间上为单调减函数
∴x=5时，函数取得最小值
| 1 |
| 5 |
∴不等式m＜
| 1 |
| x |
| 1 |
| 5 |
∴实数m的取值范围为（-∞，
| 1 |
| 5 |
故答案为：（-∞，
| 1 |
| 5 |
点评：本题考查不等式恒成立问题，解题的关键是构造函数，确定函数的单调性，求出函数的最值．
练习册系列答案
相关题目
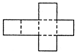如图是一个正方体纸盒的展开图，若把1，2，3，4，5，6分别填入小正方形内，按虚线折成正方体，则所得正方体相对面上两个数的和都相等的概率是（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
（文）设圆（x+3）2+（y+5）2=r2上有且只有两点到直线4x-3y=2的距离等于1．则圆的半径r的取值范围是（ ）
A、1＜r＜
| ||||
B、r＞
| ||||
C、
| ||||
| D、r＞1 |