题目内容
若平面区域上的点(x,y)满足不等式
+
≤1.则该平面区域的面积是( )
|
|
| A、30 | B、40 | C、50 | D、60 |
考点:二元一次不等式(组)与平面区域
专题:数形结合
分析:先将原不等式化去根号,再去绝对值符号,即x≥0,y≥0,x≤0,y≤0,中x、y的四种组合,化简不等式,并画图,可求平面区域面积.
解答:
 解:
解:
+
≤1即|
|+|
|≤1可化为
或
或
或
其平面区域如图.
∴面积S=
×4×5×4=40.
故选B.
 解:
解:
|
|
| x |
| 5 |
| y |
| 4 |
|
|
|
|
其平面区域如图.
∴面积S=
| 1 |
| 2 |
故选B.
点评:本题考查二元一次不等式组与平面区域问题,考查分类讨论的数学思想,是基础题.

练习册系列答案
相关题目
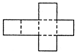 如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )
如图是一个正方体纸盒的展开图,若把1,2,3,4,5,6分别填入小正方形内,按虚线折成正方体,则所得正方体相对面上两个数的和都相等的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
已知sin(a-
)=
,则cos(
+2a)的值等于( )
| π |
| 3 |
| 1 |
| 3 |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
(文)设圆(x+3)2+(y+5)2=r2上有且只有两点到直线4x-3y=2的距离等于1.则圆的半径r的取值范围是( )
A、1<r<
| ||||
B、r>
| ||||
C、
| ||||
| D、r>1 |
 已知四边形ABCD是空间四边形,E、H分别是AB、AD的中点,F、G分别是边CB、CD上的点,且
已知四边形ABCD是空间四边形,E、H分别是AB、AD的中点,F、G分别是边CB、CD上的点,且 如图,在半径为1m的圆中作内接正六边形,再作正六边形的内切圆,又在此内切圆中作内接正六边形,如此无限继续下去,则所有这些圆的面积和S=
如图,在半径为1m的圆中作内接正六边形,再作正六边形的内切圆,又在此内切圆中作内接正六边形,如此无限继续下去,则所有这些圆的面积和S=