题目内容
6.如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
分析 (1)由题意计算$\overline{x}$、$\overline{y}$,求出回归方程的系数$\stackrel{∧}{b}$、$\stackrel{∧}{a}$,写出线性回归方程;
(2)由(1)求出的线性回归方程计算x=100时$\stackrel{∧}{y}$的值,
再计算生产100吨甲产品的生产能耗比技术改造前降低了多少.
解答 解:(1)由对照数据,计算$\overline{x}$=$\frac{1}{4}$×(3+4+5+6)=4.5,
$\overline{y}$=$\frac{1}{4}$×(2.5+3+4+4.5)=3.5;
且$\sum_{i=1}^{4}$xi2=86,$\sum_{i=1}^{4}$xiyi=66.5,
∴回归方程的系数为$\stackrel{∧}{b}$=$\frac{66.5-4×4.5×3.5}{86-4{×4.5}^{2}}$=0.7,
∴$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$=3.5-0.7×4.5=0.35,
∴所求线性回归方程为$\stackrel{∧}{y}$=0.7x+0.35;
(2)由(1)求出的线性回归方程,计算x=100时
$\stackrel{∧}{y}$=0.7×100+0.35=70.35,
∴90-70.35=19.65(吨),
预测生产100吨甲产品的生产能耗比技术改造前降低了19.65吨标准煤.
点评 本题考查了线性回归方程的求法与应用问题,是基础题.

练习册系列答案
 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
17.x>0是$\frac{1}{x}$-1>0成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.已知平面向量$\overrightarrow a,\overrightarrow b$满足$(2\overrightarrow a-\overrightarrow b)•\overrightarrow a=5$,且$|\overrightarrow a|=2,|\overrightarrow b|=3$,则向量$\overrightarrow a$与向量$\overrightarrow b$的夹角余弦值为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}$ |
15.《九章算术》中记载了公元前344年商鞅督造的一种标准量器--商鞅同方升,其主体部分的三视图如图所示,则该量器的容积为( )
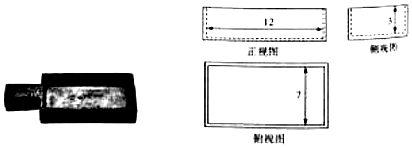

| A. | 252 | B. | 189 | C. | 126 | D. | 63 |
