题目内容
1.已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的左焦点F和上顶点B在直线$3x-\sqrt{3}y+3=0$上,A为椭圆上位于x轴上方的一点,且AF⊥x轴,M,N为椭圆C上不同于A的两点,且∠MAF=∠NAF.(1)求椭圆C的方程;
(2)设直线MN与y轴交于点D(0,d),求实数d的取值范围.
分析 (1)求得直线$3x-\sqrt{3}y+3=0$在坐标轴的交点,可得F,B的坐标,即有b,c,再由a,b,c的关系可得a的值,进而得到椭圆方程;
(2)设直线AM的斜率为k,由∠MAF=∠NAF,可得直线AM,AN关于直线AF对称,可得直线AN的斜率为-k,求得A的坐标,设出直线AM的方程,联立椭圆方程,运用韦达定理,可得M的横坐标,将k换为-k,可得N的横坐标,运用直线的斜率公式可得直线MN的斜率,进而得到直线MN的方程,联立椭圆方程,运用判别式大于0,解方程可得d的范围;再由A在直线MN上,解不等式可得d的范围,求交集,即可得到所求d的范围.
解答 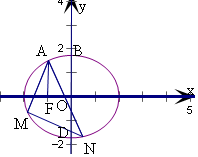 解:(1)由左焦点F和上顶点B在直线$3x-\sqrt{3}y+3=0$上,
解:(1)由左焦点F和上顶点B在直线$3x-\sqrt{3}y+3=0$上,
可得F(-1,0),B(0,$\sqrt{3}$),
即有c=1,b=$\sqrt{3}$,
a=$\sqrt{{c}^{2}+{b}^{2}}$=2,
则椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)设直线AM的斜率为k,由∠MAF=∠NAF,
可得直线AM,AN关于直线AF对称,
可得直线AN的斜率为-k,
令x=-1,可得A(-1,$\frac{3}{2}$),
设直线AM的方程为y-$\frac{3}{2}$=k(x+1),
联立椭圆方程3x2+4y2=12,
可得(3+4k2)x2+(12+8k)kx+(4k2+12k-3)=0,
设M(x1,y1),N(x2,y2),
由-x1=$\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}$,即有x1=-$\frac{4{k}^{2}+12k-3}{3+4{k}^{2}}$,
将上式中的k换为-k,可得x2=-$\frac{4{k}^{2}-12k-3}{3+4{k}^{2}}$.
y1=k(x1+1)+$\frac{3}{2}$,y2=-k(x2+1)+$\frac{3}{2}$,
则直线MN的斜率为$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{k({x}_{1}+{x}_{2}+2)}{{x}_{1}-{x}_{2}}$
=$\frac{k(-8{k}^{2}+6+6+8{k}^{2})}{-24k}$=-$\frac{1}{2}$,
由直线MN与y轴交于点D(0,d),
可得直线MN的方程为y=-$\frac{1}{2}$x+d,
代入椭圆3x2+4y2=12,
可得x2+dx+d2-3=0,
由△=d2-4(d2-3)>0,解得-2<d<2,
由A在直线MN的上方,可得$\frac{3}{2}$>-$\frac{1}{2}$×(-1)+d,
解得d<1.
可得-2<d<1.
则实数d的取值范围为(-2,1).
点评 本题考查椭圆的方程的求法,注意运用直线在坐标轴上的交点,考查直线和椭圆方程联立,运用韦达定理,考查直线斜率公式和方程的求法,以及点与直线的位置关系,考查化简整理的运算能力,属于中档题.

| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
| A. | 函数f(x)在(0,+∞)上是增函数 | B. | f(x)在(-∞,0)上是减函数 | ||
| C. | 当x=1时,f(x)取得极小值 | D. | f(0)+f(2)≥2f(1) |
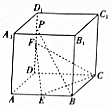 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$.