题目内容
18.在△ABC中,角A,B,C所对的边分别为a,b,c,c=$\sqrt{3}$,C=$\frac{π}{3}$,点D在边AB上,且$\overrightarrow{CD}$•$\overrightarrow{AB}$=0,则线段CD的最大值为$\frac{3}{2}$.分析 根据|$\overrightarrow{AB}$|=|$\overrightarrow{CB}-\overrightarrow{CA}$|=$\sqrt{3}$得出a2+b2=3+ab,再利用基本不等式得出ab的范围,根据面积公式得出CD关于ab的表达式,从而得出CD的最值.
解答 解:$\overrightarrow{CA}•\overrightarrow{CB}$=abcos$\frac{π}{3}$=$\frac{1}{2}ab$,
∵|$\overrightarrow{AB}$|=|$\overrightarrow{CB}-\overrightarrow{CA}$|=$\sqrt{3}$,
∴${\overrightarrow{CB}}^{2}+{\overrightarrow{CA}}^{2}-2\overrightarrow{CB}•\overrightarrow{CA}$=3,即a2+b2=3+ab,
又a2+b2≥2ab,∴3+ab≥2ab,∴ab≤3.
∵$\overrightarrow{CD}$•$\overrightarrow{AB}$=0,∴CD⊥AB,
∴S=$\frac{1}{2}absinC$=$\frac{1}{2}$×CD×c,即$\frac{\sqrt{3}}{2}$ab=$\sqrt{3}$CD,
∴CD=$\frac{1}{2}$ab≤$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了平面向量的应用与数量积运算,面积公式及基本不等式,属于中档题.

练习册系列答案
相关题目
8.已知全集U=R,集合A={x|1<x≤3},B={x|x>2},则A∩(∁UB)=( )
| A. | {x|1≤x≤2} | B. | {x|1≤x<2} | C. | {x|1<x≤2} | D. | {x|1≤x≤3} |
6.如表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据
($\stackrel{∧}{y}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$)
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
3.在正方体ABCD-A1B1C1D1中,E为DD1的中点,则下列直线中与平面ACE平行的是( )
| A. | BA1 | B. | BD1 | C. | BC1 | D. | BB1 |
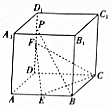 如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$.
如图,在棱长为4的正方体ABCD-A1B1C1D1中,E、F分别是AB、DD1的中点,点P是DD1上一点,且PB∥平面CEF,则四棱锥P-ABCD外接球的体积为$\frac{41\sqrt{41}}{6}π$.