题目内容
已知,ax2-x+4a=0有大于0的实数根,求实数a的取值范围.
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由题意可得a≠0,由△=1-16a2≥0,求得-
≤a≤
.再根据两根之积为4,可得方程必须有2个正实数根,故有两根之和
>0,综合可得a的范围.
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| a |
解答:
解:当a=0时,显然不满足条件,故a≠0.
∵由△=1-16a2≥0,求得-
≤a≤
.
再根据两根之积为
=4,可得方程必须有2个正实数根,故有两根之和
>0,即a>0.
综合可得a的范围为(0,
].
∵由△=1-16a2≥0,求得-
| 1 |
| 4 |
| 1 |
| 4 |
再根据两根之积为
| 4a |
| a |
| 1 |
| a |
综合可得a的范围为(0,
| 1 |
| 4 |
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若直线a与平面α不垂直,那么平面α内与直线a垂直的直线有( )
| A、0条 | B、1条 |
| C、无数条 | D、不确定 |
如图所示是一个四棱锥的三视图,则该几何体的体积为( )
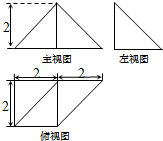

| A、4 | ||||
B、
| ||||
| C、12 | ||||
D、
|
在△ABC中,点D在BC边上,且
=2
,
=r
+s
,则r+s=( )
| CD |
| DB |
| CD |
| AB |
| AC |
A、
| ||
B、
| ||
| C、1 | ||
| D、0 |