题目内容
已知函数f（x）=sinωx+
cosωx的最小正周期为π，x∈R，ω＞0是常数．
（1）求ω的值；
（2）若f（
+
）=
，θ∈（0，
），求sin2θ．
| 3 |
（1）求ω的值；
（2）若f（
| θ |
| 2 |
| π |
| 12 |
| 6 |
| 5 |
| π |
| 2 |
考点：三角函数中的恒等变换应用,正弦函数的图象
专题：三角函数的求值,三角函数的图像与性质
分析：（1）由两角和的正弦公式化简解析式可得f（x）=2sin（ωx+
），由已知及周期公式即可求ω的值．
（2）由已知及三角函数中的恒等变换应用可得f（
+
）=2cosθ=
，可得cosθ，由θ∈（0，
），可得sinθ，sin2θ的值．
| π |
| 3 |
（2）由已知及三角函数中的恒等变换应用可得f（
| θ |
| 2 |
| π |
| 12 |
| 6 |
| 5 |
| π |
| 2 |
解答：
解：（1）∵f（x）=sinωx+
cosωx=2sin（ωx+
），
∵函数f（x）=sinωx+
cosωx的最小正周期为π，
∴T=π=
，解得：ω=2．
（2）∵f（
+
）=2sin[2（
+
）+
]=2sin（θ+
）=2cosθ=
，
∴cosθ=
，
∵θ∈（0，
），
∴sinθ=
=
，
∴sin2θ=2sinθcosθ=2×
×
=
．
| 3 |
| π |
| 3 |
∵函数f（x）=sinωx+
| 3 |
∴T=π=
| 2π |
| ω |
（2）∵f（
| θ |
| 2 |
| π |
| 12 |
| θ |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| 6 |
| 5 |
∴cosθ=
| 3 |
| 5 |
∵θ∈（0，
| π |
| 2 |
∴sinθ=
| 1-cos2θ |
| 4 |
| 5 |
∴sin2θ=2sinθcosθ=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
点评：本题主要考查了三角函数中的恒等变换应用，正弦函数的周期性，属于基本知识的考查．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
一个袋子中有号码为1、2、3、4、5大小相同的5个小球，现从袋中任意取出一个球，取出后不放回，然后再从袋中任取一个球，则第一次取得号码为奇数，第二次取得号码为偶数球的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
双曲线
-
=1的渐近线方程为（ ）
| y2 |
| 4 |
| x2 |
| 2 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
将一枚质地均匀的骰子抛掷1次，出现的点数为偶数的概率是（ ）
| A、1 | ||
B、
| ||
C、
| ||
D、
|
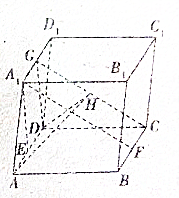如图，四棱柱ABCD=A1B1C1D1的底面是矩形，E，F，G，分别为AD，BC，A1D1的中点，A1E⊥平面ABCD，DH⊥CG，H为垂直