题目内容
已知数列{an}中,a1=1,a2=
,且an+1=
(n=2,3,4…).
(1)求数列{an}的通项公式;
(2)求证:对一切n∈N*,有
ak2<
.
| 1 |
| 4 |
| (n-1)an |
| n-an |
(1)求数列{an}的通项公式;
(2)求证:对一切n∈N*,有
| n |
 |
| k=1 |
| 7 |
| 6 |
考点:数列递推式,数列的求和
专题:等差数列与等比数列
分析:(1)当n≥2时,
=
=
-
,从而
-
=-(
-
),进而得到
[
-
]=-(1-
),由此能求出an=
,n∈N*.
(2)当k≥2时,ak2=
<
=
(
-
),由此利用裂项求和法能证明对一切n∈N*,有
ak2<
.
| 1 |
| an+1 |
| n-an |
| (n-1)an |
| n |
| (n-1)an |
| 1 |
| n-1 |
| 1 |
| nan+1 |
| 1 |
| (n-1)an |
| 1 |
| n-1 |
| 1 |
| n |
| n-1 |
 |
| k=2 |
| 1 |
| kak+1 |
| 1 |
| (k-1)ak |
| 1 |
| n-1 |
| 1 |
| 3n-2 |
(2)当k≥2时,ak2=
| 1 |
| (3k-2)2 |
| 1 |
| (3k-4)(3k-1) |
| 1 |
| 3 |
| 1 |
| 3k-4 |
| 1 |
| 3k-1 |
| n |
 |
| k=1 |
| 7 |
| 6 |
解答:
(1)解:∵a1=1,a2=
,且an+1=
(n=2,3,4…),
∴当n≥2时,
=
=
-
,
两边同时除以n,得
=
-
,
∴
-
=-(
-
),
∴
[
-
]=-
(
-
)=-(1-
)
∴
-
=-(1-
),n≥2,
∴
=
-(1-
)=
,
∴an=
,n≥2,
当n=1时,上式成立,
∴an=
,n∈N*.
(2)证明:当k≥2时,ak2=
<
=
(
-
),
∴当n≥2时,
ak2=1+
ak2<1+
[(
-
)+(
-
)+…+(
-
)]
=1+
(
-
)<1+
=
,
又n=1时,a12=1<
,
∴对一切n∈N*,有
ak2<
.
| 1 |
| 4 |
| (n-1)an |
| n-an |
∴当n≥2时,
| 1 |
| an+1 |
| n-an |
| (n-1)an |
| n |
| (n-1)an |
| 1 |
| n-1 |
两边同时除以n,得
| 1 |
| nan+1 |
| 1 |
| (n-1)an |
| 1 |
| n(n-1) |
∴
| 1 |
| nan+1 |
| 1 |
| (n-1)an |
| 1 |
| n-1 |
| 1 |
| n |
∴
| n-1 |
 |
| k=2 |
| 1 |
| kak+1 |
| 1 |
| (k-1)ak |
| n-1 |
 |
| k=2 |
| 1 |
| k-1 |
| 1 |
| k |
| 1 |
| n-1 |
∴
| 1 |
| (n-1)an |
| 1 |
| a2 |
| 1 |
| n-1 |
∴
| 1 |
| (n-1)an |
| 1 |
| a2 |
| 1 |
| n-1 |
| 3n-2 |
| n-1 |
∴an=
| 1 |
| 3n-2 |
当n=1时,上式成立,
∴an=
| 1 |
| 3n-2 |
(2)证明:当k≥2时,ak2=
| 1 |
| (3k-2)2 |
| 1 |
| (3k-4)(3k-1) |
| 1 |
| 3 |
| 1 |
| 3k-4 |
| 1 |
| 3k-1 |
∴当n≥2时,
| n |
 |
| k=1 |
| n |
 |
| k=2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 5 |
| 1 |
| 5 |
| 1 |
| 8 |
| 1 |
| 3n-4 |
| 1 |
| 3n-1 |
=1+
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3n-1 |
| 1 |
| 6 |
| 7 |
| 6 |
又n=1时,a12=1<
| 7 |
| 6 |
∴对一切n∈N*,有
| n |
 |
| k=1 |
| 7 |
| 6 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意放缩法和裂项求和法的合理运用.

练习册系列答案
相关题目
一个袋子中有号码为1、2、3、4、5大小相同的5个小球,现从袋中任意取出一个球,取出后不放回,然后再从袋中任取一个球,则第一次取得号码为奇数,第二次取得号码为偶数球的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=x
的最大值为( )
| 1-x2 |
A、
| ||||
| B、0 | ||||
C、
| ||||
D、-
|
双曲线
-
=1的渐近线方程为( )
| y2 |
| 4 |
| x2 |
| 2 |
A、y=±
| ||||
| B、y=±2x | ||||
C、y=±
| ||||
D、y=±
|
将一枚质地均匀的骰子抛掷1次,出现的点数为偶数的概率是( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
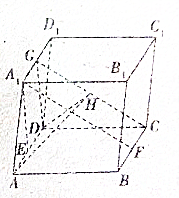 如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直
如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直