题目内容
设数列{an}满足:a1=5,an+1+4an=5,(n∈N*)
(I)是否存在实数t,使{an+t}是等比数列?
(Ⅱ)设数列bn=|an|,求{bn}的前2014项和S2014.
(I)是否存在实数t,使{an+t}是等比数列?
(Ⅱ)设数列bn=|an|,求{bn}的前2014项和S2014.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(Ⅰ)由已知得an+1=-4an+5,令an+1+t=-4(an+t),得t=-1,从而求出存在这样的实数t=-1,使{an+t}是等比数列.
(Ⅱ)由an-1=4•(-4)n-1.得bn=|an|=
,由此能求出{bn}的前2014项和S2014.
(Ⅱ)由an-1=4•(-4)n-1.得bn=|an|=
|
解答:
解:(Ⅰ)由an+1+4an=5,得an+1=-4an+5,
令an+1+t=-4(an+t),…(2分)
得an+1=-4an-5t,则-5t=5,解得t=-1,…(4分)
从而an+1-1=-4(an-1).
又a1-1=4,∴{an-1}是首项为4,公比为-4的等比数列,
∴存在这样的实数t=-1,使{an+t}是等比数列.…(6分)
(Ⅱ)由(Ⅰ)得an-1=4•(-4)n-1.
∴bn=|an|=
,(8分)
∴S2015=(1+4)+(42-1)+(1+43)+…+(42014-1)
=4+42+43+…+42014
=
=
.…(12分)
令an+1+t=-4(an+t),…(2分)
得an+1=-4an-5t,则-5t=5,解得t=-1,…(4分)
从而an+1-1=-4(an-1).
又a1-1=4,∴{an-1}是首项为4,公比为-4的等比数列,
∴存在这样的实数t=-1,使{an+t}是等比数列.…(6分)
(Ⅱ)由(Ⅰ)得an-1=4•(-4)n-1.
∴bn=|an|=
|
∴S2015=(1+4)+(42-1)+(1+43)+…+(42014-1)
=4+42+43+…+42014
=
| 4(1-42014) |
| 1-4 |
=
| 42015-4 |
| 3 |
点评:本题考查是否存在使得数列为等比数列的实数的判断与求法,考查数列的前2014项和的求法,是中档题,解题时要注意等比数列的性质的合理运用.

练习册系列答案
相关题目
将一枚质地均匀的骰子抛掷1次,出现的点数为偶数的概率是( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
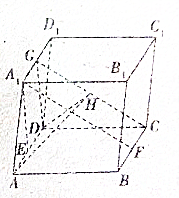 如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直
如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直