题目内容
已知f(2x+1)=x2-2x.
(1)求f(x);
(2)f(3)的值.
(1)求f(x);
(2)f(3)的值.
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:利用换元法,令2x+1=t,则x=
(t-1),即可求出函数的解析式,再代入值,求出函数值即可.
| 1 |
| 2 |
解答:
解:(1)令2x+1=t,则x=
(t-1),
∴f(t)=
(t-1)2-2(t-1)=
t2-
t+
,
∴f(x)=
x2-
x+
;
(2)由(1)知f(3)=
×32-
×3+
=-3.
| 1 |
| 2 |
∴f(t)=
| 1 |
| 4 |
| 1 |
| 4 |
| 5 |
| 2 |
| 9 |
| 4 |
∴f(x)=
| 1 |
| 4 |
| 5 |
| 2 |
| 9 |
| 4 |
(2)由(1)知f(3)=
| 1 |
| 4 |
| 5 |
| 2 |
| 9 |
| 4 |
点评:本题考查了函数的解析式的求法和函数值得问题,关键是利用换元法,属于基础题

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案
相关题目
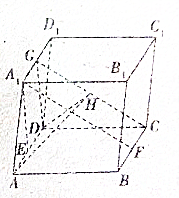 如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直
如图,四棱柱ABCD=A1B1C1D1的底面是矩形,E,F,G,分别为AD,BC,A1D1的中点,A1E⊥平面ABCD,DH⊥CG,H为垂直(1)求证:A1F∥平面CDG
(2)求证:CG⊥平面ADH.
在△ABC中,已知a=5,b=4,∠C=60°,则C边长为( )
A、
| ||
B、
| ||
C、
| ||
| D、5 |