题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,若2cos2
=1-cos2C,c-b=4,且a,b,c成等差数列,则△ABC的面积为 .
| A+B |
| 2 |
考点:余弦定理,等比数列的通项公式
专题:解三角形
分析:t通过三角函数的内角和以及二倍角公式求出C的值,利用已知条件以及余弦定理,等差数列,通过解方程求出a,b即可求解三角形的面积.
解答:
解:∵cos
=cos(
-
)=-sin
,cos2C=2cos2C-1,
∴2cos2(
)+cos2C=2sin2
+cos2C=(1-cosC)+2cos2C-1=1,
整理可得cosC=-
,或cosC=0
又C为三角形的内角,
则C=
;
c-b=4…①,且a,b,c成等差数列,∴2b=a+c…②,c2=a2+b2-2abcosC=a2+b2+ab…③,
解①②③可得a=6,b=10,
△ABC的面积S=
absinC=15
,
故答案为:15
.
| A+B |
| 2 |
| π |
| 2 |
| C |
| 2 |
| C |
| 2 |
∴2cos2(
| A+B |
| 2 |
| C |
| 2 |
整理可得cosC=-
| 1 |
| 2 |
又C为三角形的内角,
则C=
| 2π |
| 3 |
c-b=4…①,且a,b,c成等差数列,∴2b=a+c…②,c2=a2+b2-2abcosC=a2+b2+ab…③,
解①②③可得a=6,b=10,
△ABC的面积S=
| 1 |
| 2 |
| 3 |
故答案为:15
| 3 |
点评:本题考查余弦定理,等差数列,二倍角的余弦函数,诱导公式的应用,是难度不大的综合题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
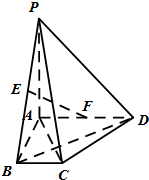 如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=PA=2,E,F分别为PB,AD的中点.
如图,在四棱锥P-ABCD中,PA⊥面ABCD,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=PA=2,E,F分别为PB,AD的中点.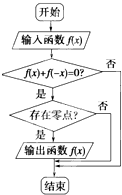 某程序框图如图所示,现输入四个函数(1)f(x)=x2,(2)f(x)=
某程序框图如图所示,现输入四个函数(1)f(x)=x2,(2)f(x)=