题目内容
20.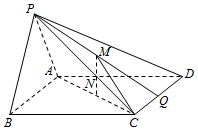 如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.(Ⅰ)证明:MN∥平面PAB;
(Ⅱ)证明:平面MNC⊥平面ABCD.
分析 (Ⅰ)连BD,交AC于N,连结BQ,取BQ中点E,连结ME,NE,则EM∥PB,EN∥DQ,从而平面PAB∥平面EMN,由此能证明MN∥平面PAB.
(Ⅱ)取AB中点O,连结PO,QO,推导出PO⊥平面ABCD,从而MN⊥平面ABCD,由此能证明平面MNC⊥平面ABCD.
解答 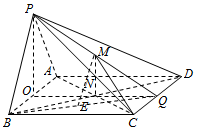 证明:(Ⅰ)连BD,交AC于N,连结BQ,取BQ中点E,连结ME,NE,
证明:(Ⅰ)连BD,交AC于N,连结BQ,取BQ中点E,连结ME,NE,
∵四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点,
∴N是BD中点,∴EM∥PB,EN∥DQ,
∵DQ∥AB,∴EN∥AB,
∵PB∩AB=B,EM∩EN=E,
PB、AB?平面PAB,EM、EN?平面EMN,
∴平面PAB∥平面EMN,
∵MN?平面EMN,∴MN∥平面PAB.
(Ⅱ)取AB中点O,连结PO,QO,
∵在四棱锥P-ABCD中,平面PAB⊥底面ABCD,PA=PB,四边形ABCD是菱形,
N为AC的中点,M是△PCD的中线PQ的中点,
∴PO⊥AB,MN∥PO,∴PO⊥平面ABCD,
∴MN⊥平面ABCD,
∵MN?平面MNC,∴平面MNC⊥平面ABCD.
点评 本题考查线面平行的证明,考查面面垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10. 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
(Ⅰ)在如表中作出这些数据的频率分布直方图:
(Ⅱ)若将频率视为概率,从参与节目的报账人中随机抽取3位(看作有放回的抽样),求账单总额在[3000,4000)内的报账人数X的分布列、数学期望、与方差.
 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
(Ⅱ)若将频率视为概率,从参与节目的报账人中随机抽取3位(看作有放回的抽样),求账单总额在[3000,4000)内的报账人数X的分布列、数学期望、与方差.
5.已知|$\overrightarrow{a}$|2=1,|$\overrightarrow{b}$|2=2,($\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{a}$=0,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
10.已知数列{an}的前n项和为Sn,则“{an}为常数列”是“?n∈N*,Sn=nan”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
 广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图的频率分布直方图.问:
广场舞是现代城市群众文化、娱乐发展的产物,其兼具文化性和社会性,是精神文明建设成果的一个重要指标和象征.2015年某高校社会实践小组对某小区广场舞的开展状况进行了年龄的调查,随机抽取了40名广场舞者进行调查,将他们年龄分成6段:[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图的频率分布直方图.问: