题目内容
12.已知椭圆M:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,点A是椭圆M与圆C:x2+(y-2$\sqrt{2}$b)2=$\frac{4}{9}$m2在第一象限的交点,且点A到F2的距离等于$\frac{1}{3}$m,若椭圆M上一动点到点F1与到点C的距离之差的最大值为2a-m,则椭圆M的离心率为$\frac{1}{2}$.分析 求得圆C的圆心和半径,运用椭圆的定义和三点共线的性质,可得当P在线段CF2上时,|PF2|+|PC|取得最小值|CF2|,即有|PF1|-|PC|的最大值为2a-m=2a-|CF2|,再由直线CF2:$\frac{x}{c}$+$\frac{y}{2\sqrt{2}b}$=1,联立圆的方程,求得交点A,代入椭圆方程,运用离心率公式即可得到所求值.
解答 解:圆C:x2+(y-2$\sqrt{2}$b)2=$\frac{4}{9}$m2的圆心C(0,2$\sqrt{2}$b),半径为$\frac{2}{3}$m,m>0,
|AF2|=$\frac{1}{3}$m,可得|AC|+|AF2|=m,
由椭圆上一动点P到点F1与到点C的距离之差的最大值为2a-m,
由椭圆的定义可得|PF1|-|PC|=2a-|PF2|-|PC|=2a-(|PF2|+|PC|),
当P在线段CF2上时,|PF2|+|PC|取得最小值|CF2|,
即有|PF1|-|PC|的最大值为2a-m=2a-|CF2|,
则|CF2|=m,可得|CF2|=|AC|+|AF2|=m=$\sqrt{{c}^{2}+8{b}^{2}}$,
即有A在线段CF2上,
由CF2:$\frac{x}{c}$+$\frac{y}{2\sqrt{2}b}$=1,联立圆的方程x2+(y-2$\sqrt{2}$b)2=$\frac{4}{9}$m2,
解得x=$\frac{2}{3}$c,y=$\frac{2\sqrt{2}}{3}$b.
即A($\frac{2}{3}$c,$\frac{2\sqrt{2}}{3}$b),代入椭圆方程可得:
$\frac{4{c}^{2}}{9{a}^{2}}$+$\frac{8}{9}$=1,即a=2c,
则e=$\frac{c}{a}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查椭圆的定义和方程及性质,考查直线和圆的位置关系,注意联立直线方程和圆方程求交点,考查三点共线的性质以及椭圆离心率的求法,属于中档题.

 发散思维新课堂系列答案
发散思维新课堂系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | 0 | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | 1 |
| A. | c<b<a | B. | a<b<c | C. | b<a<c | D. | b<c<a |
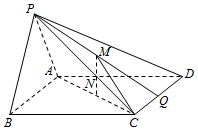 如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.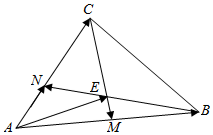 如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.
如图所示,在△ABC中,点M为AB的中点,且AN=$\frac{1}{2}$NC,BN与CM相交于点E,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,试以$\overrightarrow{a}$,$\overrightarrow{b}$为基底表示$\overrightarrow{AE}$.