题目内容
10.已知数列{an}的前n项和为Sn,则“{an}为常数列”是“?n∈N*,Sn=nan”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据数列前n项和与数列通项的关系以及充分条件和必要条件的定义进行判断即可.
解答 解:若{an}为常数列,则d=0,则Sn=nan成立,即充分性成立,
若Sn=nan,则当n≥2时,an=Sn-Sn-1=nan-(n-1)an-1,
即(n-1)an-1=(n-1)an,
则an-1=an,则{an}为常数列,即必要性成立.
故“{an}为常数列”是“?n∈N*,Sn=nan”的充要条件,
故选:C.
点评 本题主要考查充分条件和必要条件的判断,根据数列前n项和与数列通项的关系是解决本题的关键.

练习册系列答案
相关题目
1.已知f(x)为偶函数,且在(-∞,0]上单调递减,若a=f(30.3),b=f(log23),c=f(log${\;}_{\frac{1}{3}}$$\frac{1}{9}$),则a,b,c的大小关系是( )
| A. | c<b<a | B. | a<b<c | C. | b<a<c | D. | b<c<a |
19.若实数x,y满足$\left\{\begin{array}{l}{x≥3}\\{y≤3}\\{{x}^{2}+{y}^{2}=25}\end{array}\right.$,则2x+2y的最大值为( )
| A. | 10$\sqrt{2}$ | B. | 14 | C. | 5$\sqrt{6}$ | D. | 12 |
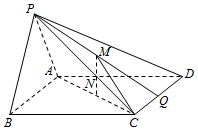 如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.