题目内容
10. 《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:
《幸福账单》是一档集情感故事、才艺秀、大型游戏、现场互动等多类元素的综艺大型互动游戏类节目.以普通人讲述手中账单背后的故事,并参与因此而量身为其定制的大型游戏,来赢得账单报销的形式,讲述了人与人之间的真情,展现了当今百姓生活中的万般幸福之态.某机构随机抽取100个参与节目的报账人的账单总额作为样本进行分析研究,由此得到如下频数分布表:| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
(Ⅱ)若将频率视为概率,从参与节目的报账人中随机抽取3位(看作有放回的抽样),求账单总额在[3000,4000)内的报账人数X的分布列、数学期望、与方差.
分析 (Ⅰ)由已知先作出频率分布表为,由此能作出频率分布直方图.
(Ⅱ)将频率视为概率从参与节目的报账人中随机抽取3位(看作有放回的抽样),由频率分布直方图得账单总额在[3000,4000)内的报账人数X~B(3,0.1),由此能求出X的分布列、数学期望、与方差.
解答 解:(Ⅰ)由已知得频率分布表为:
| 报账人的账单总额(元) | [0,1000) | [1000,2000) | [2000,3000) | [3000,4000) | [4000,5000) | [5000,6000) |
| 频数 | 24 | 12 | 32 | 10 | 14 | 8 |
| 频率 | 0.24 | 0.12 | 0.32 | 0.10 | 0.14 | 0.08 |
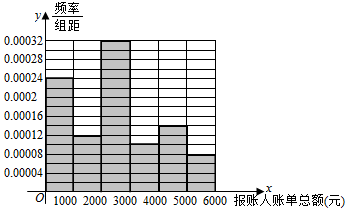
(Ⅱ)将频率视为概率从参与节目的报账人中随机抽取3位(看作有放回的抽样),
由频率分布直方图得账单总额在[3000,4000)内的报账人数X~B(3,0.1),
∴P(X=0)=${C}_{3}^{0}×0.{9}^{3}$=0.729,
P(X=1)=${C}_{3}^{1}×0.1×0.{9}^{2}$=0.243,
P(X=2)=${C}_{3}^{2}×0.{1}^{2}×0.9$=0.027,
P(X=3)=${C}_{3}^{3}×0.{1}^{3}$=0.0001,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.729 | 0.243 | 0.027 | 0.0001 |
∴EX=3×0.1=0.3,
DX=3×0.1×(1-0.1)=0.27.
点评 本题考查频率分布直方图的作法,考查离散型随机变量的分布列、数学期望、方差的作法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
1.已知命题p,q,则“¬p或q为假”是“p且¬q为真”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.某工厂新研发的一种产品的成本价是4元/件,为了对该产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下6组数据:
(Ⅰ)若90≤x+y<100,就说产品“定价合理”,现从这6组数据中任意抽取2组数据,2组数据中“定价合理”的个数记为X,求X的数学期望;
(Ⅱ)求y关于x的线性回归方程,并用回归方程预测在今后的销售中,为使工厂获得最大利润,该产品的单价应定为多少元?(利润L=销售收入-成本)
附:线性回归方程$\hat y=\hat bx+\hat a$中系数计算公式:$\hat b=\frac{{\sum_{i=1}^n{(\;{x_i}-\overline x\;)(\;{y_i}-\overline y\;)}}}{{\sum_{i=1}^n{{{(\;{x_i}-\overline x\;)}^2}}}}$,$\hat a=\overline y-\hat b\;\overline x$,其中$\overline x$、$\overline y$表示样本均值.
| 单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(Ⅱ)求y关于x的线性回归方程,并用回归方程预测在今后的销售中,为使工厂获得最大利润,该产品的单价应定为多少元?(利润L=销售收入-成本)
附:线性回归方程$\hat y=\hat bx+\hat a$中系数计算公式:$\hat b=\frac{{\sum_{i=1}^n{(\;{x_i}-\overline x\;)(\;{y_i}-\overline y\;)}}}{{\sum_{i=1}^n{{{(\;{x_i}-\overline x\;)}^2}}}}$,$\hat a=\overline y-\hat b\;\overline x$,其中$\overline x$、$\overline y$表示样本均值.
15.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象与x轴的一个交点$(-\frac{π}{12},0)$到其相邻的一条对称轴的距离为$\frac{π}{4}$.若$f(\frac{π}{12})=\frac{3}{2}$,则函数f(x)在$[0,\frac{π}{2}]$上的最小值为( )
| A. | $\frac{1}{2}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
2.在△ABC中,角A,B,C所对的边分别为a,b,c,若$\sqrt{3}acosB+bsinA=0$,则B=( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
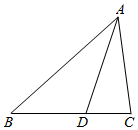 如图,在△ABC中,记$\overrightarrow{BA}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b$,∠B=$\frac{π}{3}$,AB=8,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.
如图,在△ABC中,记$\overrightarrow{BA}=\overrightarrow a,\overrightarrow{BC}=\overrightarrow b$,∠B=$\frac{π}{3}$,AB=8,点D在BC边上,且CD=2,cos∠ADC=$\frac{1}{7}$.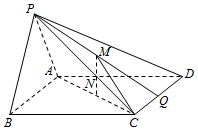 如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.
如图,在四棱锥P-ABCD中,平面PAB⊥底面ABCD,其中PA=PB,四边形ABCD是菱形,N为AC的中点,M是△PCD的中线PQ的中点.