已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1.求过它的焦点且垂直于实轴的弦长．题目和参考答案——青夏教育精英家教网——

题目内容

9．已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1，求过它的焦点且垂直于实轴的弦长．

分析求出双曲线的a，b，c，可令x=5，代入双曲线的方程，可得弦长．

解答解：双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的a=4，b=3，c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{16+9}$=5，
可令x=5，代入双曲线的方程，可得y=±3$\sqrt{\frac{25}{16}-1}$=±$\frac{9}{4}$，
即有过它的焦点且垂直于实轴的弦长为$\frac{18}{4}$=$\frac{9}{2}$．

点评本题考查双曲线的方程和性质，主要考查过焦点垂直于x轴的弦长的求法，考查运算能力，属于基础题．

练习册系列答案

周报经典英语周报系列答案

假期作业吉林教育出版社系列答案

口算题天天练系列答案

正大图书练测考系列答案

一本必胜系列答案

进阶集训系列答案

尖子生单元测试系列答案

轻松假期行暑假用书系列答案

世纪百通主体课堂小学课时同步练习系列答案

经纶学典棒棒堂系列答案

相关题目

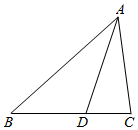如图，在△ABC中，记$\overrightarrow{BA}=\overrightarrow a，\overrightarrow{BC}=\overrightarrow b$，∠B=$\frac{π}{3}$，AB=8，点D在BC边上，且CD=2，cos∠ADC=$\frac{1}{7}$．
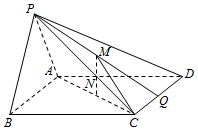（Ⅰ）试用$\overrightarrow a，\overrightarrow b$表示$\overrightarrow{DA}$；
（Ⅱ）若以B点为坐标原点，BC所在的直线为x轴（正方向为向右）建立平面直角坐标系，使得点A落在第一象限．点P（x，y）在△ABC三边围成的区域（含边界）上，设$\overrightarrow{BP}=m\overrightarrow a+n\overrightarrow b（m，n∈R）$，求m-n的最大值．

如图，在四棱锥P-ABCD中，平面PAB⊥底面ABCD，其中PA=PB，四边形ABCD是菱形，N为AC的中点，M是△PCD的中线PQ的中点．
（Ⅰ）证明：MN∥平面PAB；
（Ⅱ）证明：平面MNC⊥平面ABCD．

17．已知在直角坐标系xOy中，圆C的参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}\right.$（θ为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为ρcos（θ-$\frac{π}{4}$）=$\sqrt{2}$．求圆C的普通方程和直线l的直角坐标方程．

4．已知极坐标系的极点与直角坐标系的原点重合，极轴与x轴的非负半轴重合，若曲线C的极坐标方程为ρ=6cosθ+2sinθ，直线l的参数方程为$\left\{\begin{array}{l}{x=1-\sqrt{2}t}\\{y=2+\sqrt{2}t}\end{array}\right.$（t为参数）．
（1）求曲线C的直角坐标方程与直线l的普通方程；
（2）设点Q（1，2），直线l与曲线C交于A，B两点，求|QA|•|QB|的值．

14．已知平面上三个向量$\overrightarrow{a}$、$\overrightarrow{b}$、$\overrightarrow{c}$，给出下列说法：
①若$\overrightarrow{c}$=$\overrightarrow{a}$$+\overrightarrow{b}$，则$\overrightarrow{a}$、$\overrightarrow{b}$可以作为基底；
②若$\overrightarrow{a}$$∥\overrightarrow{b}$，且|$\overrightarrow{a}$|=|$\overrightarrow{b}$|，则$\overrightarrow{a}$=$\overrightarrow{b}$；
③若$\overrightarrow{a}$=$λ\overrightarrow{b}$，则|$\overrightarrow{a}$|=λ|$\overrightarrow{b}$|；
④若$\overrightarrow{a}$$+\overrightarrow{b}+\overrightarrow{c}$=$\overrightarrow{0}$，则|$\overrightarrow{c}$|≤|$\overrightarrow{a}$|+|$\overrightarrow{b}$|．
其中正确说法的序号是④（写出所有正确的序号）

1．已知f（x）为偶函数，且在（-∞，0]上单调递减，若a=f（3^0.3），b=f（log₂3），c=f（log${\;}_{\frac{1}{3}}$$\frac{1}{9}$），则a，b，c的大小关系是（　　）

18．在明朝程大位《算法统宗》中有这样的一首歌谣：“远看巍巍塔七层，红光点点倍加增，共灯三百八十一，请问尖头几盏灯”．这首古诗描述的这个宝塔其古称浮屠，本题一共有7层．每层悬挂的红灯数是上一层的2倍，共有381盏灯，问塔顶有几盏灯？你算出顶层有3盏灯．

19．若实数x，y满足$\left\{\begin{array}{l}{x≥3}\\{y≤3}\\{{x}^{2}+{y}^{2}=25}\end{array}\right.$，则2x+2y的最大值为（　　）