题目内容
解关于x的不等式|x+7|-|3x-4|+
-1>0.
| 2 |
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:分类讨论,去掉绝对值,分别求出每种情况下不等式的解集,再取并集,即得所求.
解答:
解:当x>
时,原不等式转化为x+7-(3x-4)+
-1>0,解得x<5+
,综合可得
<x<5+
.
当-7≤x≤
时,原不等式转化为x+7-(4-3x)+
-1>0,解得x>
,综合可得
≤
.
当x<-7时,原不等式转化为-(x+7)-(4-3x)+
-1>0,解得x>6-
(舍去).
综上,不等式的解集为{x|
≤x<5+
}.
| 4 |
| 3 |
| 2 |
| ||
| 2 |
| 4 |
| 3 |
| ||
| 2 |
当-7≤x≤
| 4 |
| 3 |
| 2 |
-2-
| ||
| 4 |
-2-
| ||
| 4 |
| 4 |
| 3 |
当x<-7时,原不等式转化为-(x+7)-(4-3x)+
| 2 |
| ||
| 2 |
综上,不等式的解集为{x|
-2-
| ||
| 4 |
| ||
| 2 |
点评:本题主要考查绝对值不等式的解法,体现了分类讨论、转化的数学思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知f(x)=
,则f(3)=( )
|
| A、3 | B、2 | C、4 | D、5 |
执行如图的程序,若输入的x=2,则输出的所有x的值的和为( )


| A、6 | B、21 | C、101 | D、126 |
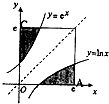 如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )
如图,在边长为e(e为自然对数的底数)的正方形区域的A处于C处各有一个通信基站,其信号覆盖范围分别为如图所示的阴影区域.该正方形区域内无其它信号来源且这两个基站工作正常,若在该正方形区域内随机选择一个地点,则该地点无信号的概率为( )A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
已知某四棱台的三视图如图所示,则该四棱台的体积是( )


A、
| ||
| B、4 | ||
C、
| ||
| D、6 |
已知命题p:“若直线ax+y+1=0与直线ax-y+2=0垂直,则a=1”;命题q:“a
<b
”是“a<b”的充要条件,则( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、p真,q假 |
| B、“p∧q”真 |
| C、“p∨q”真 |
| D、“p∨q”假 |