题目内容
16.正四面体ABCD中,E、F分别为边AB、BD的中点,则异面直线AF、CE所成角的余弦值为$\frac{1}{6}$.分析 画出立体图形,根据中点找平行线,把所求的异面直线角转化为一个三角形的内角来计算.
解答  解:如图,连接CF,取BF的中点M,连接CM,EM,
解:如图,连接CF,取BF的中点M,连接CM,EM,
则ME∥AF,故∠CEM即为所求的异面直线角.
设这个正四面体的棱长为2,
在△ABD中,AF=$\sqrt{3}$=CE=CF,EM=$\frac{\sqrt{3}}{2}$,CM=$\frac{\sqrt{13}}{2}$.
∴cos∠CEM=$\frac{\frac{3}{4}+3-\frac{13}{4}}{2×\frac{\sqrt{3}}{2}×\sqrt{3}}$=$\frac{1}{6}$.
故答案为$\frac{1}{6}$.
点评 本题考查空间点、线、面的位置关系及学生的空间想象能力、求异面直线角的能力.在立体几何中找平行线是解决问题的一个重要技巧,这个技巧就是通过三角形的中位线找平行线,如果试题的已知中涉及到多个中点,则找中点是出现平行线的关键技巧.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
6.若实数x,y满足不等式$\left\{\begin{array}{l}{2x+y+2≥0}\\{x+y-1≤0}\\{y≥m}\end{array}\right.$,且x-y的最大值为5,则实数m的值为( )
| A. | 0 | B. | -1 | C. | -2 | D. | -5 |
4.已知曲线C:y=ex和直线l:ax+by=0,若直线l上有且只有两个关于y轴的对称点在曲线C上,则$\frac{b}{a}$的取值范围是( )
| A. | (-∞,-e) | B. | (-∞,$\frac{1}{e}$) | C. | (0,$\frac{1}{e}$) | D. | (e,+∞) |
11.已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
5.一企业从某条生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到如下的频率分布表:
(Ⅰ)作出样本的频率分布直方图,并估计该技术指标值x的平均数和众数;
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
| x | [11,13) | [13,15) | [15,17) | [17,19) | [19,21) | [21,23) |
| 频数 | 2 | 12 | 34 | 38 | 10 | 4 |
(Ⅱ)若x<13或x≥21,则该产品不合格.现从不合格的产品中随机抽取2件,求抽取的2件产品中技术指标值小于13的产品恰有一件的概率.
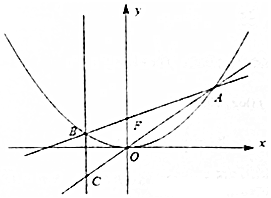 已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.
已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.