题目内容
已知函数f(x)=
sin2xsinφ+
cosφ-
sin(
+φ)(0<x<π),其图象过点(
,
).
(Ⅰ)求φ的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的
,纵坐标不变,得到函数y=g(x)的图象,求函数g(x)在[0,
]上的最大值和最小值.
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(Ⅰ)求φ的值;
(Ⅱ)将函数y=f(x)的图象上各点的横坐标缩短到原来的
| 1 |
| 2 |
| π |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换,三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(Ⅰ)把已知的函数解析式化简变形,然后由函数图象过点(
,
)列式求得φ值;
(Ⅱ)首先利用函数图象的平移得到函数y=g(x)的解析式,然后根据x∈[0,
]求得相位的范围,则g(x)在[0,
]上的最大值和最小值可求.
| π |
| 6 |
| 1 |
| 2 |
(Ⅱ)首先利用函数图象的平移得到函数y=g(x)的解析式,然后根据x∈[0,
| π |
| 4 |
| π |
| 4 |
解答:
解:(Ⅰ)∵函数图象过点(
,
),
∴有
=
sin2×
sinφ+cos2
cosφ-
sin(
+φ)(0<φ<π),
有1=
sinφ+
cosφ-cosφ=sin(φ+
),
∴φ+
=
,解得φ=
;
(Ⅱ)由(Ⅰ)知φ=
,
∴f(x)=
sin2x+
×
-
=
sin(2x+
),
∴g(x)=
sin(4x+
),
∵x∈[0,
],
∴4x+
∈[
,
],
∴当4x+
=
时,g(x)取最大值
;
当4x+
=
时,g(x)取最小值-
.
| π |
| 6 |
| 1 |
| 2 |
∴有
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 6 |
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
有1=
| ||
| 2 |
| 3 |
| 2 |
| π |
| 6 |
∴φ+
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
(Ⅱ)由(Ⅰ)知φ=
| π |
| 3 |
∴f(x)=
| ||
| 4 |
| 1 |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 6 |
∴g(x)=
| 1 |
| 2 |
| π |
| 6 |
∵x∈[0,
| π |
| 4 |
∴4x+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
∴当4x+
| π |
| 6 |
| π |
| 2 |
| 1 |
| 2 |
当4x+
| π |
| 6 |
| 7π |
| 6 |
| 1 |
| 4 |
点评:本题考查了由y=Asin(ωx+φ)的部分图象求函数解析式,关键是φ的求解,考查了三角函数值域的求法,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
推理过程“大前提:□,小前提:四边形ABCD是矩形,结论:四边形ABCD的对角线相等.”应补充的大前提是( )
| A、矩形的对角线相等 |
| B、等腰梯形的对角线相等 |
| C、正方形的对角线相等 |
| D、矩形的对边平行且相等 |
若函数f(x)为定义在R上的奇函数,且在(0,+∞)内是增函数,又f(2)=0,则不等式xf(x)<0的解集为( )
| A、(-2,0)∪(2,+∞) |
| B、(-∞,-2)∪(0,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-2,0)∪(0,2) |
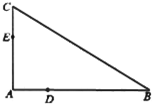 如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.
如图,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x-mn=0的两个根.